Home
Class 12
MATHS
Find the area of the region in which poi...

Find the area of the region in which points satisfy
`3 le |x| + |y| le 5.`

Text Solution

Verified by Experts

The correct Answer is:
32 sq. units
We have `3 le |x|+|y| le 5`.
`|x|+|y| le 5` means that points lie inside the square endpoints of whose diagonal are `(+-5,0) " and " (0,+-5).`
`|x|+|y| ge 3` means that points lie outside the square endpoints of whose diagonal are `(+-3,0) " and " (0,+-3).`
So, common region is as shown in the figure.

`"Area of region" =4((1)/(2) xx 5 xx 5-(1)/(2) xx 3 xx 3) = 32 "sq.units"`
Promotional Banner

Topper's Solved these Questions

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.5|8 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.6|5 Videos

  • STRAIGHT LINES

    CENGAGE|Exercise Exercise 2.3|7 Videos

  • STRAIGHT LINE

    CENGAGE|Exercise Multiple Correct Answers Type|8 Videos

  • THEORY OF EQUATIONS

    CENGAGE|Exercise JEE Advanced Previous Year|9 Videos

Similar Questions

Explore conceptually related problems

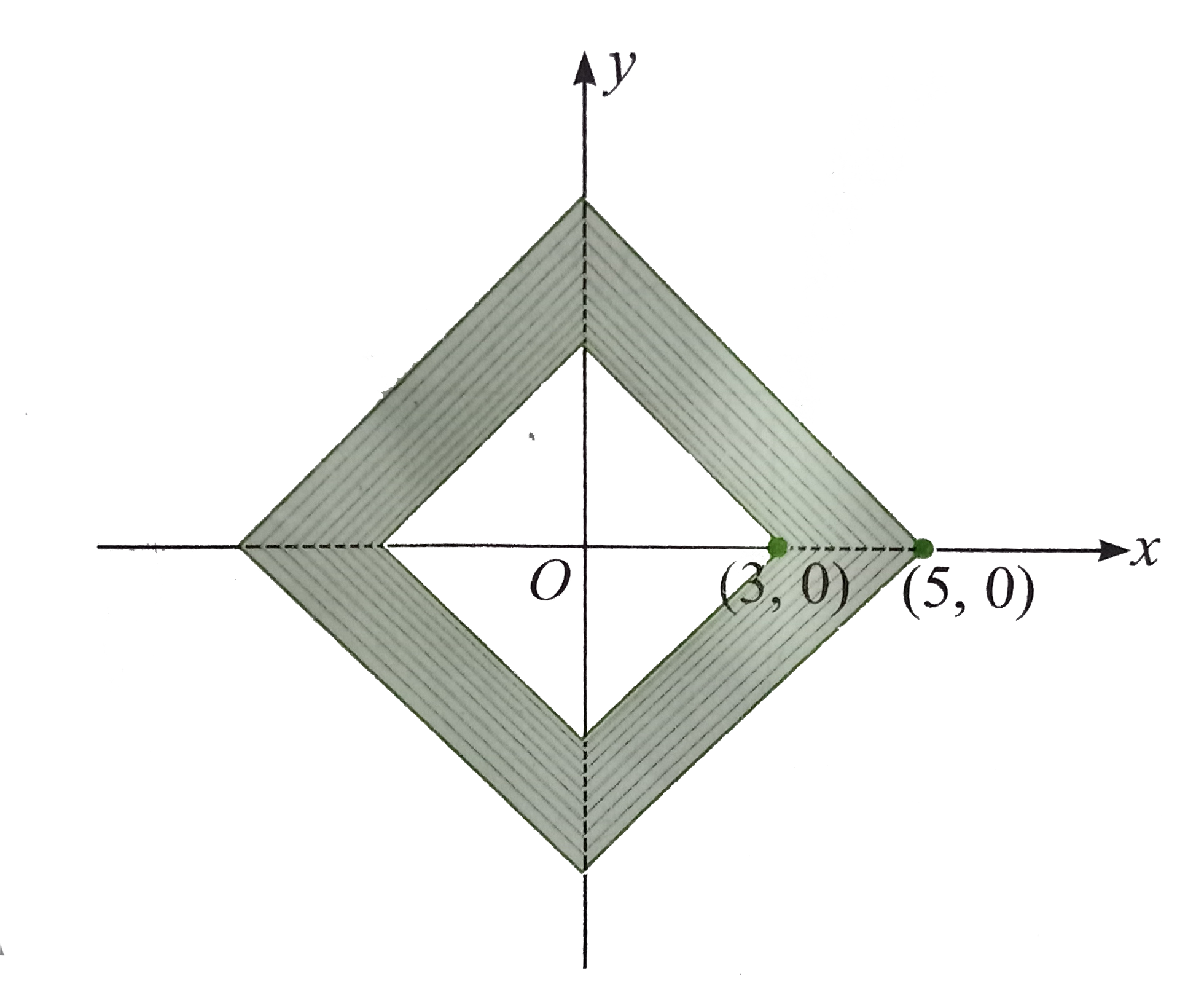
Find the area of the region formed by the points satisfying |x| + |y| + |x+y| le 2.

Sketch the region of the points satisfying max. {|x|, |y|} le 4 .

Find the area of the region which is inside the parabola satisfying the condition |x-2 y|+|x+2y|le 8 and xy ge 2 .

Find the area of the region [ (x,y) :x^2 le y le x )

Find the area of the region {(x,y) : x^2 le y le x }

Find the area of the region {(x,y):x^2 le y le |x| }.

The area of the region on place bounded by max (|x|,|y|) le 1/2 is

Find the area of the region given by x+y le 6, x^2+y^2 le 6y and y^2 le 8x .