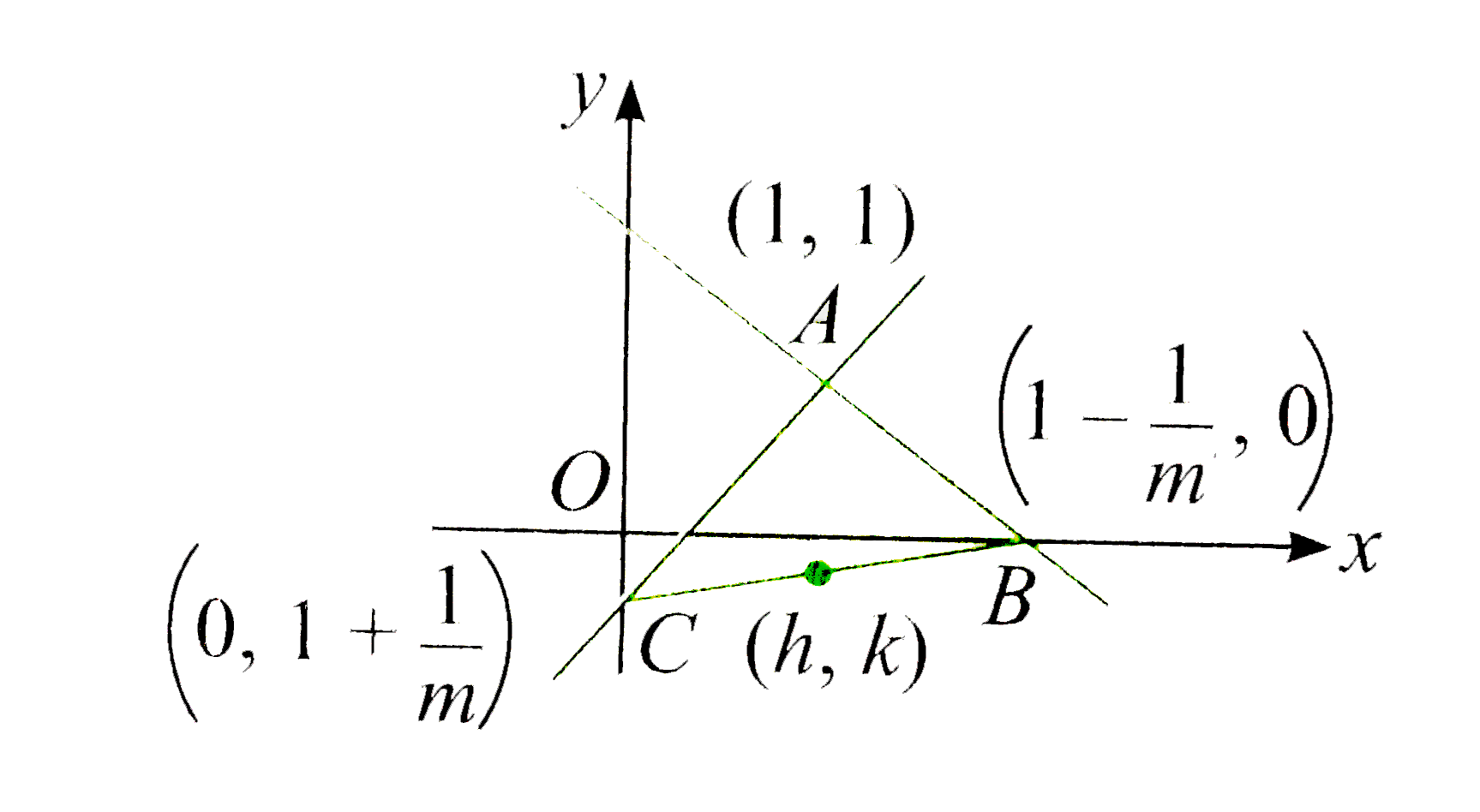A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
STRAIGHT LINES
CENGAGE|Exercise Exercise (Multiple)|30 VideosSTRAIGHT LINES
CENGAGE|Exercise Exercise (Comprehension)|27 VideosSTRAIGHT LINES
CENGAGE|Exercise Exercise 2.6|5 VideosSTRAIGHT LINE
CENGAGE|Exercise Multiple Correct Answers Type|8 VideosTHEORY OF EQUATIONS
CENGAGE|Exercise JEE Advanced Previous Year|9 Videos
Similar Questions
Explore conceptually related problems
CENGAGE-STRAIGHT LINES-Exercise (Single)
- A line with positive rational slope, passes through the point A(6,0) a...
Text Solution
|
- The line 'x + 3y - 2 = 0' bisects the angle between a pair of straight...
Text Solution
|
- Given A-=(1,1) and A B is any line through it cutting the x-axis at Bd...
Text Solution
|
- The number of possible straight lines passing through point(2,3) and f...
Text Solution
|
- Two parallel lines lying in the same quadrant make intercepts a and b ...
Text Solution
|
- The line L1-=4x+3y-12=0 intersects the x-and y-axies at Aa n dB , resp...
Text Solution
|
- A beam of light is sent along the line x-y=1 , which after refracting ...
Text Solution
|
- The number of integral values of m for which the x-coordinate of the p...
Text Solution
|
- If the sum of the distances of a point from two perpendicular lines in...
Text Solution
|
- The equation of set of lines which are at a constant distance 2 units...
Text Solution
|
- The lines y = m1x, y = m2x, and y = m3x make equal in- tercepts on the...
Text Solution
|
- The condition on aa n db , such that the portion of the line a x+b y-1...
Text Solution
|
- The area of the triangle formed by the lines y= ax, x+y-a=0, and y-axi...
Text Solution
|
- The line x/a+y/b=1 meets the x-axis at A , the y-axis at B , and the l...
Text Solution
|
- The lien x/3+y/4=1 meets the y- and x-a x y s at Aa n dB , respectivel...
Text Solution
|
- The area of a parallelogram formed by the lines a x+-b x+-c=0 is (c^2)...
Text Solution
|
- One diagonal of a square is 3x-4y+8=0 and one vertex is (-1,1), then t...
Text Solution
|
- In an isoceles triangle OAB , O is the origin and OA=OB=6 . The equati...
Text Solution
|
- A straight line through the origin 'O' meets the parallel lines 4x +2y...
Text Solution
|
- The coordinates of the foot of the perpendicular from the point (2,3) ...
Text Solution
|