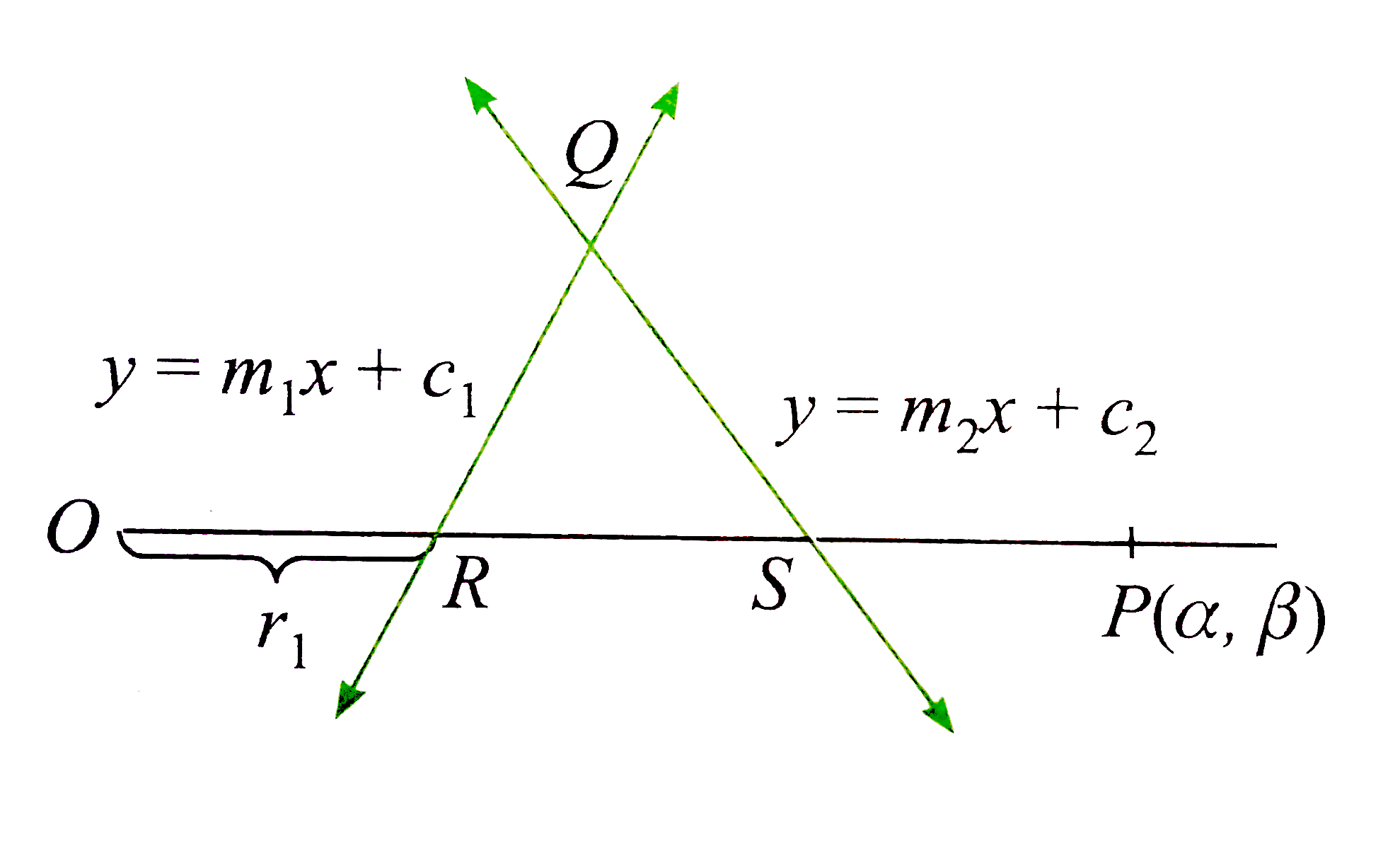Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let L1=0a n dL2=0 be two fixed lines. A variable line is drawn through...
Text Solution
|
- Let L1=0a n dL2=0 be two fixed lines. A variable line is drawn through...
Text Solution
|
- The straight line through a fixed point (2,3) intersects the coordinat...
Text Solution
|
- Two lines l and m interset at the O and P is Point on a line n Passing...
Text Solution
|
- In two circles , one circle passes through the centre O of the other c...
Text Solution
|
- A variable line is drawn through the origin O. Two points A and B same...
Text Solution
|
- Through a given point O a straigt line is drwan to cut two given strai...
Text Solution
|
- Two lines l and m interset at the O and P is Point on a line n Passing...
Text Solution
|
- Let L1=0a n dL2=0 be two fixed lines. A variable line is drawn through...
Text Solution
|