Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
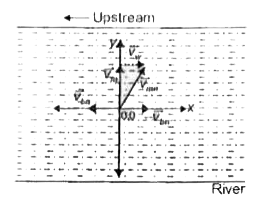
- A man swims across a river with speed of 5 km h^(-1) ( in still water...
Text Solution
|
- A man swims across a river with speed of 5 km h^(-1) ( in still water...
Text Solution
|
- A man can swin with speed 6 km/h in still water. If he tries of swim a...
Text Solution
|
- If the speed of a boat in still water is 8 km/h and the rate of stream...
Text Solution
|
- The river flows at 4 km/h. A boat can go downstream thrice as fast as ...
Text Solution
|
- A man can row downstream at 12 km/h and upstream at 8 km/h. What is th...
Text Solution
|
- A man can row downstream at 12 km/h and upstream at 8 kn/h what is the...
Text Solution
|
- A man swims across a river with speed of 5 km h^(-1) ( in still water)...
Text Solution
|
- A man can swin with speed 6 km/h in still water. If he tries of swim a...
Text Solution
|