Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS-Exercise
- Evlute [limt(x to 0)(tan^(-1)x)/(x)], where [*] re[resemts the greates...
Text Solution
|
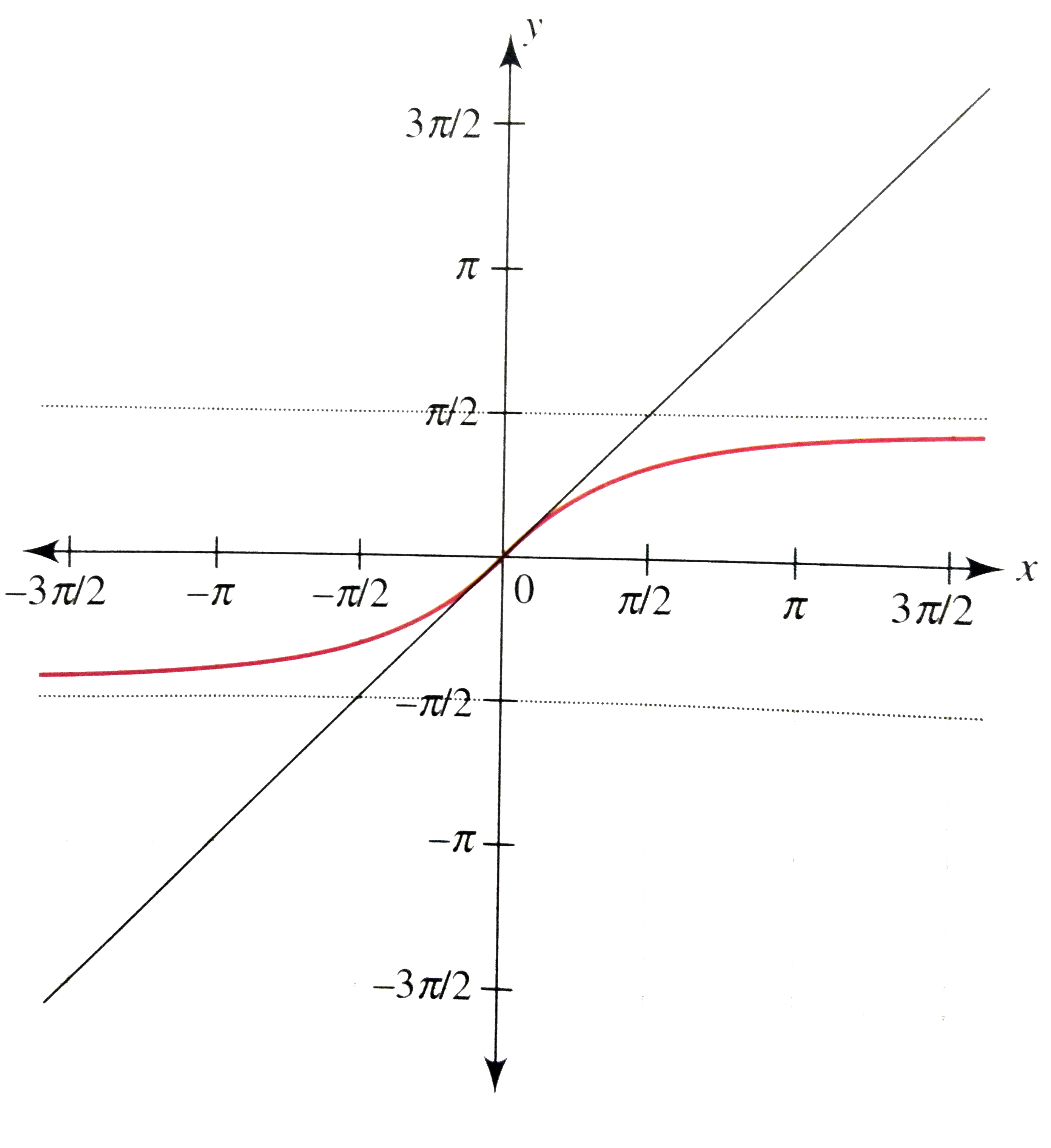
- Draw the graph of y=tan^(-1)x+cot^(-1)x
Text Solution
|
- Find the number of real solution to the equation 3cos^(-1)x-pix-pi/2=0
Text Solution
|
- Evalute [lim(xto0) (sin^(-1)x)/(x)]=1, where[*] represets the greatest...
Text Solution
|
- Solve tan^(-1)xgtcot^(-1)x graphically. Also find where f(x) = max. [t...
Text Solution
|
- Match the colums.
Text Solution
|
- Drew the graph of y=cos^(-1)sqrt(log([x])(|x|/x)) where [*] represents...
Text Solution
|
- Find the value of int(0)^(100pi)sin^(-1)(sin x)dx.
Text Solution
|
- Draw the graph of y=sin^(-1),(1)/(x)
Text Solution
|
- Draw the graph of y=sin^(-1)(x^(2))
Text Solution
|
- Draw the graph of y=cos^(-1)x^(3)" and compare with the graph of "y=co...
Text Solution
|
- Draw the graph of y=cos^(-1)(2^(x)).
Text Solution
|
- Draw the graph of y=cos^(-1){x}," where "{*}" represetns the fractiona...
Text Solution
|
- If cos^(-1)(cos x)=(n-x)/n,xge0, has seven roots, then find values of ...
Text Solution
|
- Draw the graph of f(x)=[cot^(-1)x]," where "[*] represents the greate...
Text Solution
|
- Draw the graph of y="cosec"("cosec"^(-1)x)" or "y=sec(sec^(-1)x).
Text Solution
|
- Draw the graph of f(x) =cot^(-1)((2-|x|)/(2+|x|)).
Text Solution
|
- Draw the graph of y=sin^(-1)(2xsqrt(1-x^(2)))
Text Solution
|
- Draw the graph of y=tan^(-1)((3x-x^(3))/(1-3x^(2))).
Text Solution
|