Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-COORDINATE SYSYEM -Exercise 1.4
- The line joining the points (x ,2x)a n d(3,5) makes an obtuse angle...
Text Solution
|
- If the line passing through (4,3)a n d(2,k) is parallel to the line...
Text Solution
|
- Triangle ABC lies in the cartesian plane and has an area of 70 sq. uni...
Text Solution
|
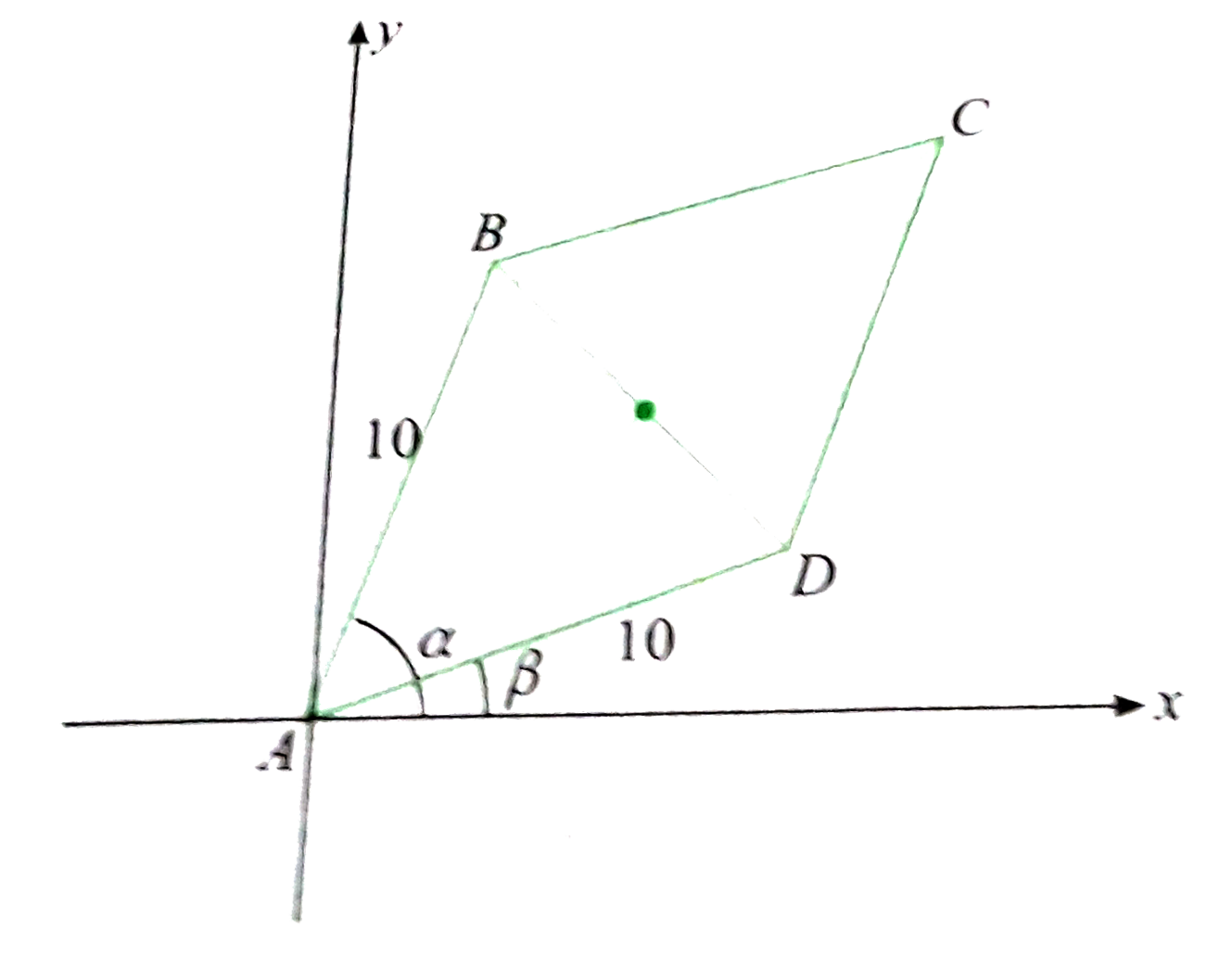
- For a given point A(0,0), ABCD is a rhombus of side 10 units where slo...
Text Solution
|
- The line joining the points A(2,1), and B(3,2) is perpendicular to the...
Text Solution
|
- Find the angle between the line joining the points (1,-2), (3,2) and t...
Text Solution
|
- The othocenter of DeltaABC with vertices B(1,-2) and C(-2,0) is H(3,-1...
Text Solution
|
- The medians AD and BE of the triangle with vertices A(0,b),B(0,0) and ...
Text Solution
|