A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
BANSAL-TEST PAPERS-PHYSICS
- Suppose a player hits several baseballs. Which baseball will be in the...
Text Solution
|
- A girl is standing on ground near a horizontally moving conveyor belt....
Text Solution
|
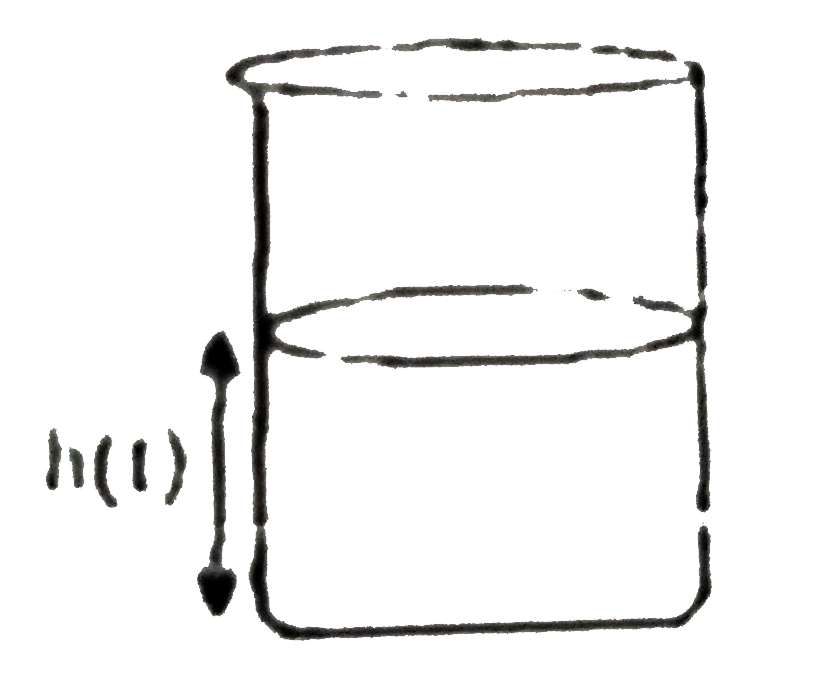
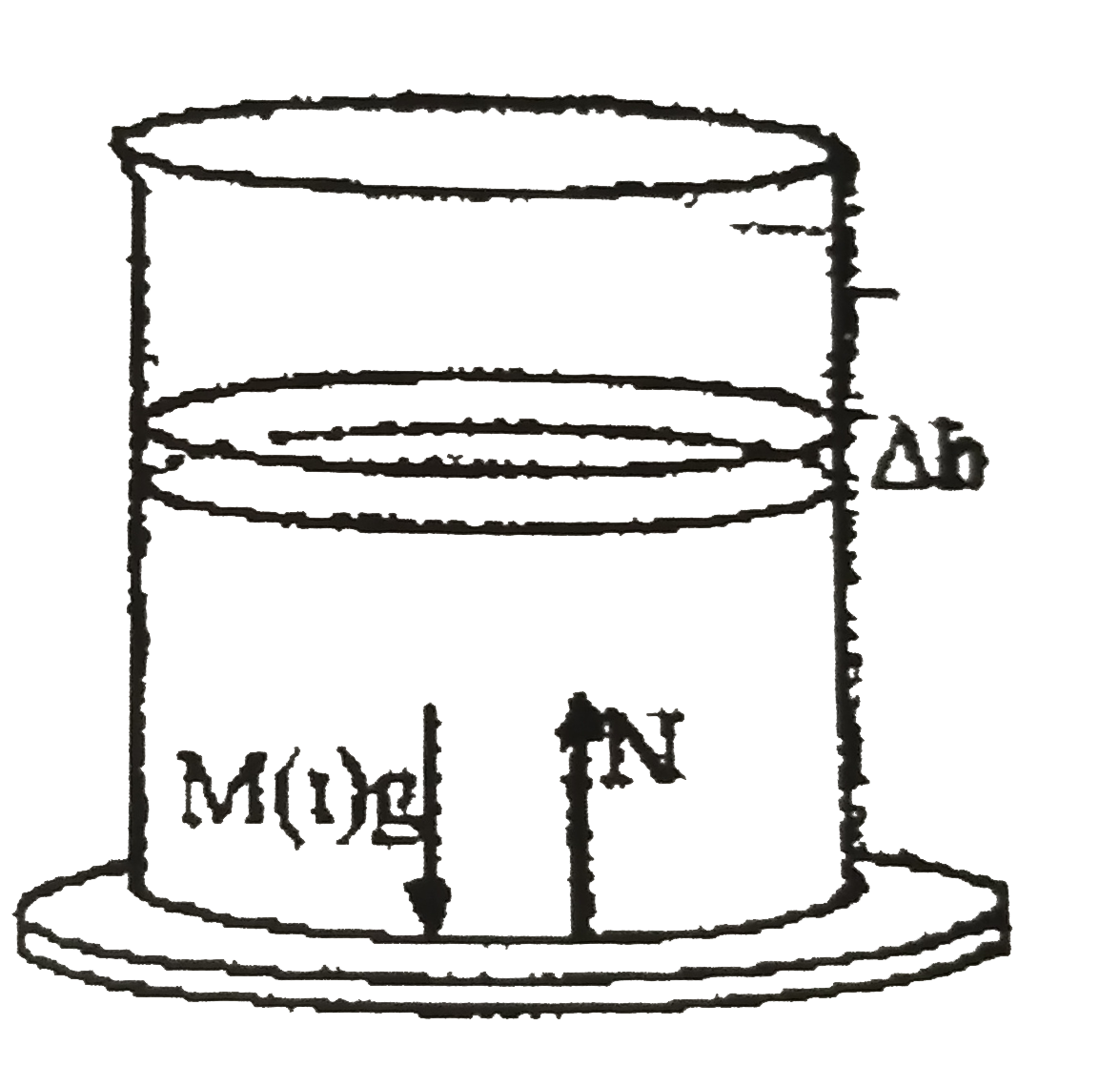
- An initially empty beaker, in the shape of a cylinder with cross secti...
Text Solution
|
- An initially empty beaker, in the shape of a cylinder with cross secti...
Text Solution
|
- An initially empty beaker, in the shape of a cylinder with cross secti...
Text Solution
|
- A constant force F acts for 1 sec, on a body of mass 1kg moving with ...
Text Solution
|
- An observer A is at rest in gournd frame, observer B is moving with co...
Text Solution
|
- A book leans against a crate on a table. Neither is moving . Which of ...
Text Solution
|
- A roller coaster starts from A, 120m above the ground, as shown. Assum...
Text Solution
|
- A block of mass 2kg is sliding on a smooth surface. At t=0, its speed ...
Text Solution
|
- Under the condition shown in figure. Find out the minimum value of hor...
Text Solution
|
- Two equal masses m are attached by a string. One mass lies at radial d...
Text Solution
|
- Find the velocity (in m/s) with wich a block of mass 1 kg must be hori...
Text Solution
|
- A uniform rod of length 10meters and mass 20 kilograms is balanced on ...
Text Solution
|
- Consdier the equation (d)/(dt)[intvecF.dvecs]=A[vecF.vecp] Then dime...
Text Solution
|
- A heavy particle is projected with a velocity at an acure angle with t...
Text Solution
|
- A particle is projected at an angle of 45^(@) with the horizontal with...
Text Solution
|
- Two identical rings each of mass m with their planes mutually perpendi...
Text Solution
|
- Two balls of same mass are dropped from the same height h, on to the f...
Text Solution
|
- A block of mass m is placed on a rough horizontal floor and it is pull...
Text Solution
|