Similar Questions
Explore conceptually related problems
Recommended Questions
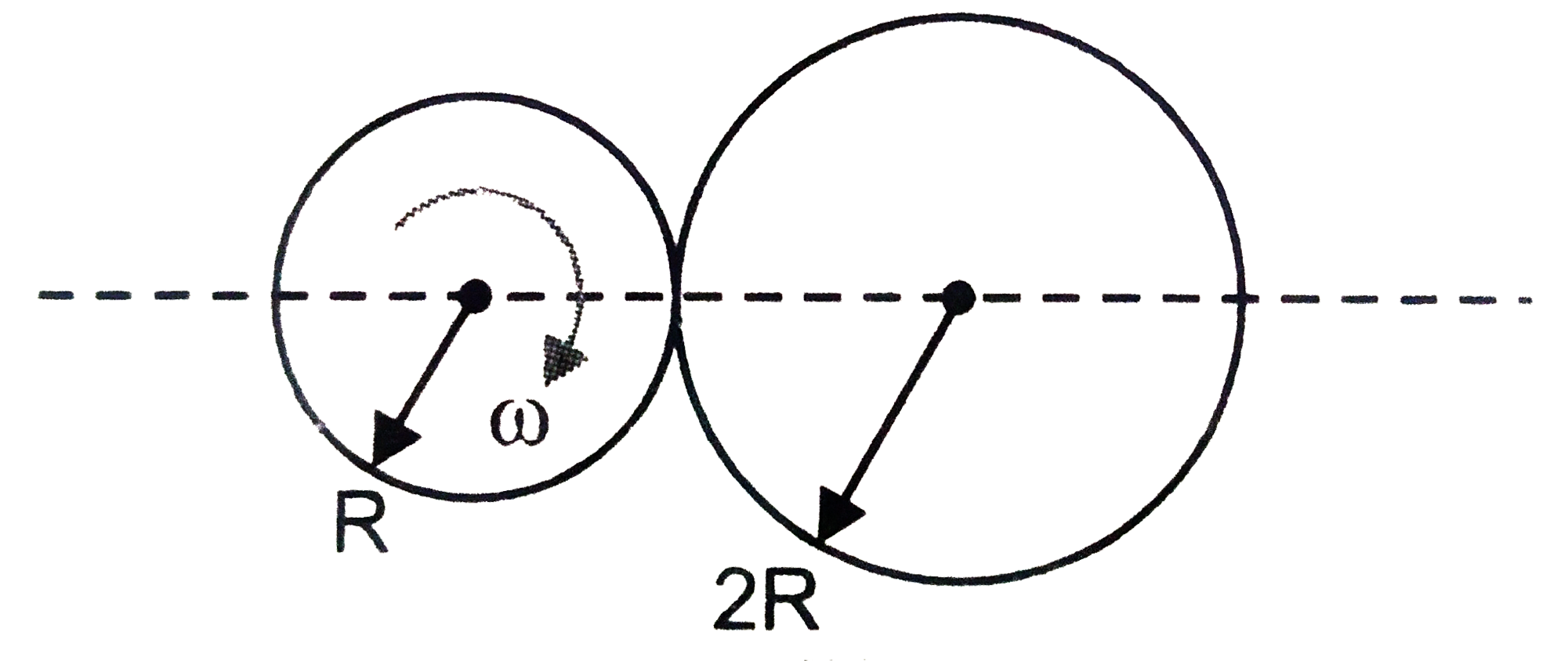
- Two discs of radii R and 2R are pressed against each other. Initially,...
Text Solution
|
- Find the position of instantaneous centre of rotation and angular velo...
Text Solution
|
- Two discs of radii R and 2R are pressed against eachother. Initially, ...
Text Solution
|
- A horizontal disc rotates with a constant angular velocity omega=6.0ra...
Text Solution
|
- A uniform circular disc of radius R is rotating about its own axis wit...
Text Solution
|
- A disc of moment of inertia la is rotating in a horizontal plane about...
Text Solution
|
- A disc with moment of inertia I is rotating with some angular speed. S...
Text Solution
|
- A circular disc is rotating about its natural axis with angular veloci...
Text Solution
|
- A constant power is supplied to a rotating disc. The relationship of a...
Text Solution
|