Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
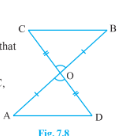
- In Fig. 7.8, O A\ =\ O Ba n d\ O D\ =\ O C. Show that (i) DeltaA O D~=...
Text Solution
|
- In Fig. 7.8, O A\ =\ O Ba n d\ O D\ =\ O C. Show that (i) DeltaA O D~=...
Text Solution
|
- In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at ...
Text Solution
|
- A B C D is a trapezium in which A B C D . The diagonals A C and...
Text Solution
|
- A B C D IS A PARALLELOGRAM AND O is any point in its interior. Prov...
Text Solution
|
- If O\ a n d\ O^(prime) are circumcentre and orthocentre of \ A B C ,\ ...
Text Solution
|
- In the given figure (not to scale), O is the centre of the circle. A,B...
Text Solution
|
- In fig. O is the center of the circle. Find the value of x. ltimg sr...
Text Solution
|
- In Fig. 7.8, O A\ =\ O Ba n d\ O D\ =\ O C. Show that (i) DeltaA O D~=...
Text Solution
|