Similar Questions
Explore conceptually related problems
Recommended Questions
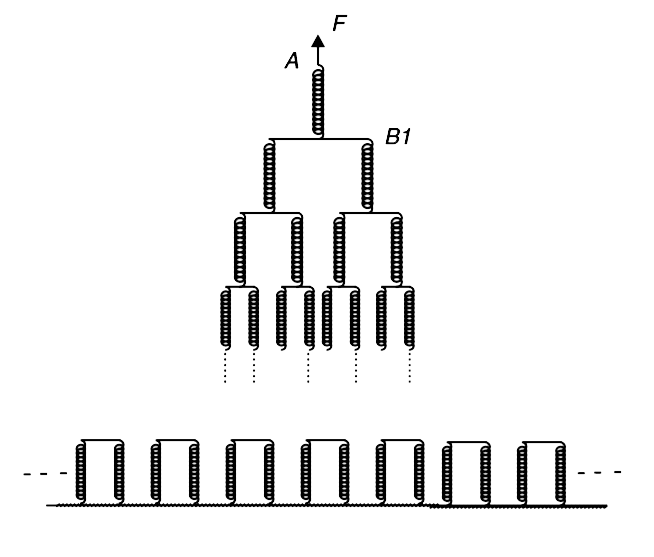
- The fig. shows an infinite tower of identical springs each having forc...
Text Solution
|
- spring of force constant k clamped rigidly at onoe end and a mass m at...
Text Solution
|
- The fig. shows an infinite tower of identical springs each having forc...
Text Solution
|
- A spring of force constant K rests on a smooth floor, with one end fix...
Text Solution
|
- Figure shows tow cases. In first case a spring (spring constant K) is ...
Text Solution
|
- The force of two springs is constant k ,. One end of a spring is conne...
Text Solution
|
- Force constants of two springs are k1 and k2 One end of a spring is co...
Text Solution
|
- Force constants of two springs are k1 and k2 . One end of a spring is ...
Text Solution
|
- Figure 14.26 (a) shows a spring of force constant k clamped rigidly at...
Text Solution
|