Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
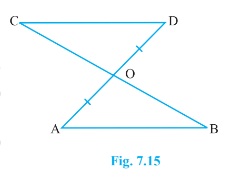
- Line-segment AB is parallel to another line-segment CD. O is the mid-...
Text Solution
|
- Line-segment AB is parallel to another line-segment CD. O is the mid-...
Text Solution
|
- In Figure, line segment A B is parallel to another line segment C D . ...
Text Solution
|
- In Figure, line segments A B is parallel to another line segment C...
Text Solution
|
- In Figure, line segments A B is parallel to another line segment C...
Text Solution
|
- रेखाखंड AB एक अन्य रेखाखंड CD के समांतर है और O रेखाखंड AD का मध्य-बिं...
Text Solution
|
- रेखाखंड AB एक अन्य रेखाखंड CD के समांतर है और O रेखाखंड AD का मध्य बिं...
Text Solution
|
- Line-segment AB is parallel to another line-segment CD. O is the mid-p...
Text Solution
|
- Line-segment AB is parallel to another line-segment CD. O is the mid-p...
Text Solution
|