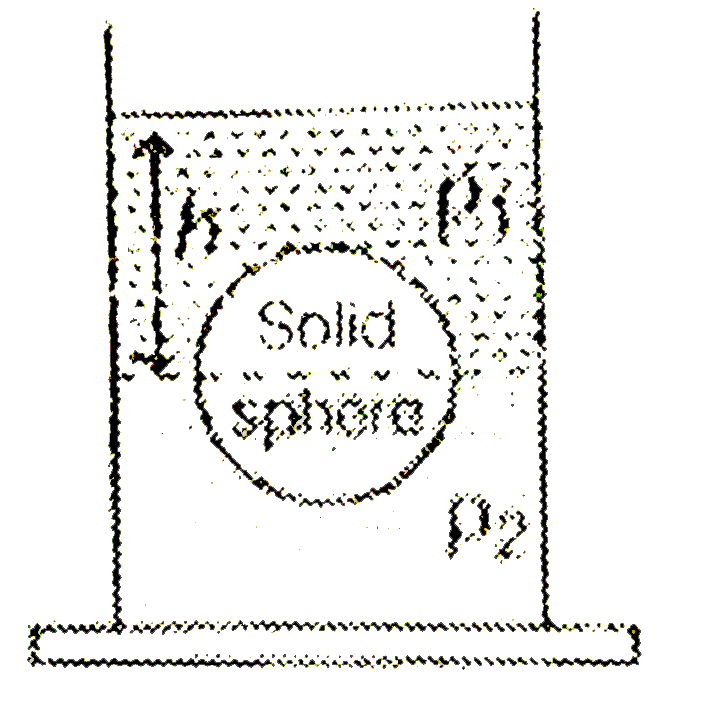Similar Questions
Explore conceptually related problems
Recommended Questions
- A solid sphere of radius r is floating at the interface of two immisci...
Text Solution
|
- A solid uniform ball of volume V floats on the interface of two immisc...
Text Solution
|
- A solid sphere having volume V and density rho floats at the interface...
Text Solution
|
- A solid uniform ball having volume V and density rho floats at the int...
Text Solution
|
- A body of density rho floats with a volume V(1) of its total volume V ...
Text Solution
|
- A solid sphere of radius r is floating at the interface of two immisci...
Text Solution
|
- Assertion : A solid is floating in a liquid of density rho(1). When th...
Text Solution
|
- A thin uniform tube is bent into a circle of radius r in the vertical ...
Text Solution
|
- A uniform sphere of density rho floats at the interface of two liquids...
Text Solution
|