Home
Class 9
MATHS
ABC and DBC are two isosceles triangles...

ABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that`/_A B D\ =/_A C D`

Text Solution

Verified by Experts


Given: `ABC` and `DBC` are isosceles triangles
To Prove: `∠ABD = ∠ACD`
Let's join point A and point B.
...
Promotional Banner

Topper's Solved these Questions

  • TRIANGLES

    NCERT|Exercise EXERCISE 7.5|4 Videos

  • SURFACE AREAS AND VOLUMES

    NCERT|Exercise EXERCISE 13.8|10 Videos

Similar Questions

Explore conceptually related problems

In Figure,ABC and DBC are two isosceles triangles on the same base BC such that AB=AC and DB=CD. Prove that /_ABD=/_ACD

△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that (i) △ABD≅△ACD (ii) △ABP≅△ACP (iii) AP bisects ∠A as well as △D . (iv) AP is the perpendicular bisector of BC.

In Figure,ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC .Prove that /_ABD=/_ACD

Delta ABC and Delta DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that

triangle ABC and triangle DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles

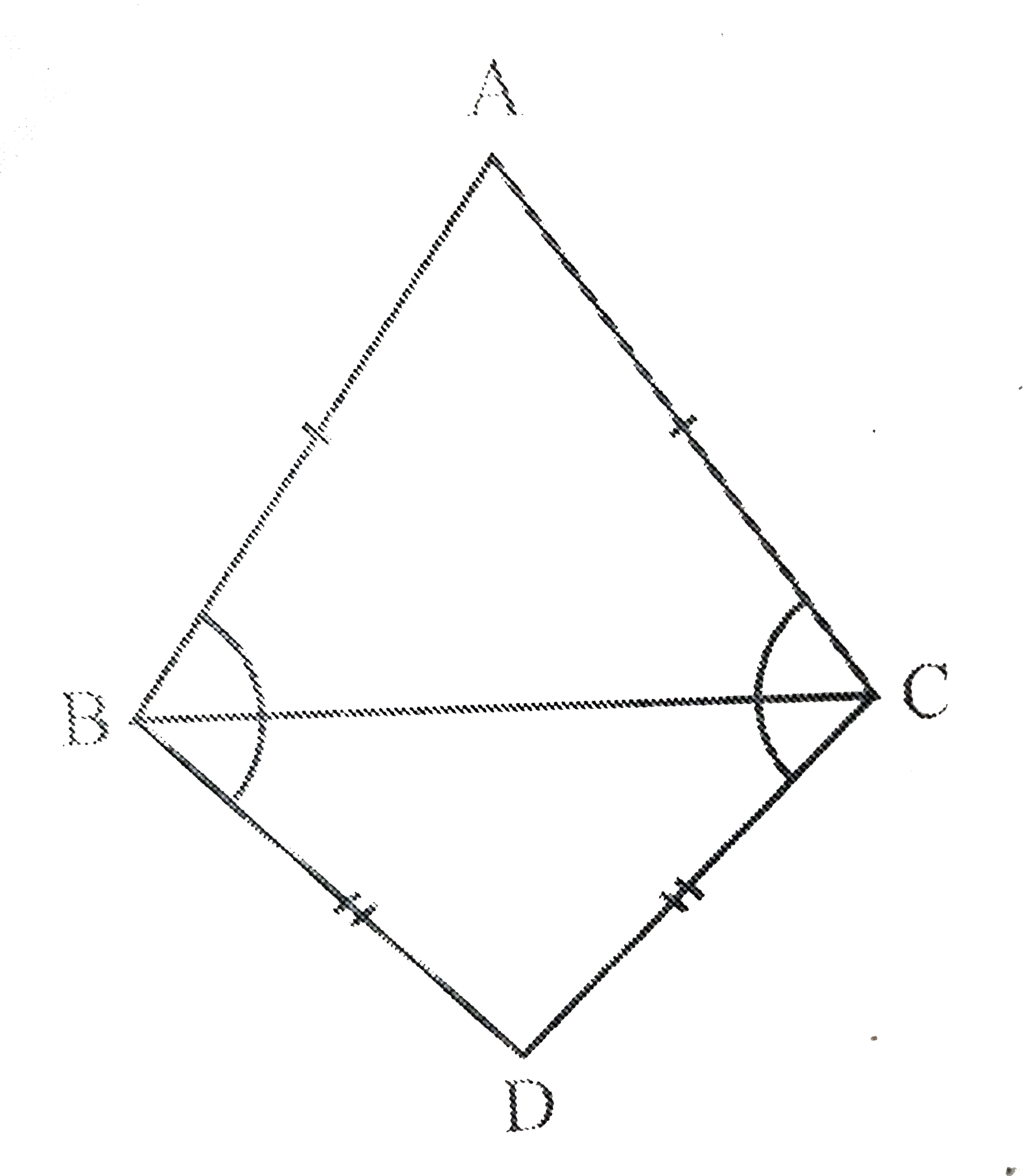
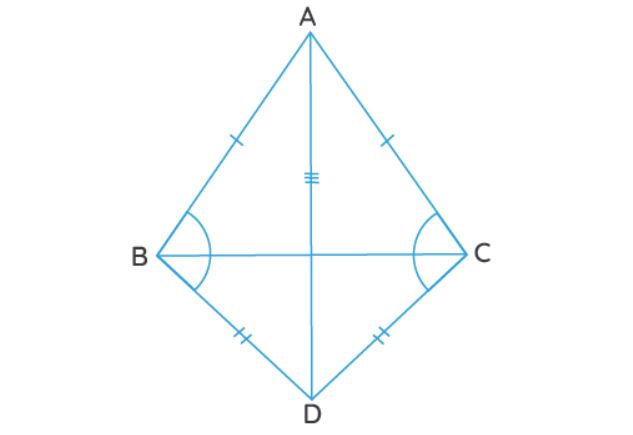
A B C\ a n d\ D B C are two isosceles triangles on the same bas B C and vertices A\ a n d\ D are on the same side of B C . If A D is extended to intersect B C at P , show that A P bisects "\ "/_A as well as /_D A P is the perpendicular bisector of B C

DeltaA B C and DeltaD B C are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) \ DeltaA B D~=DeltaA C D (ii) DeltaA B P~=DeltaACP (iii) AP bisects ∠ A as well as ∠ D (iv) AP is the perpendicular bisector of BC

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that DeltaABD~=DeltaACD

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that DeltaABP~=DeltaACP

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that AP bisects angleA as well as angleD .