A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
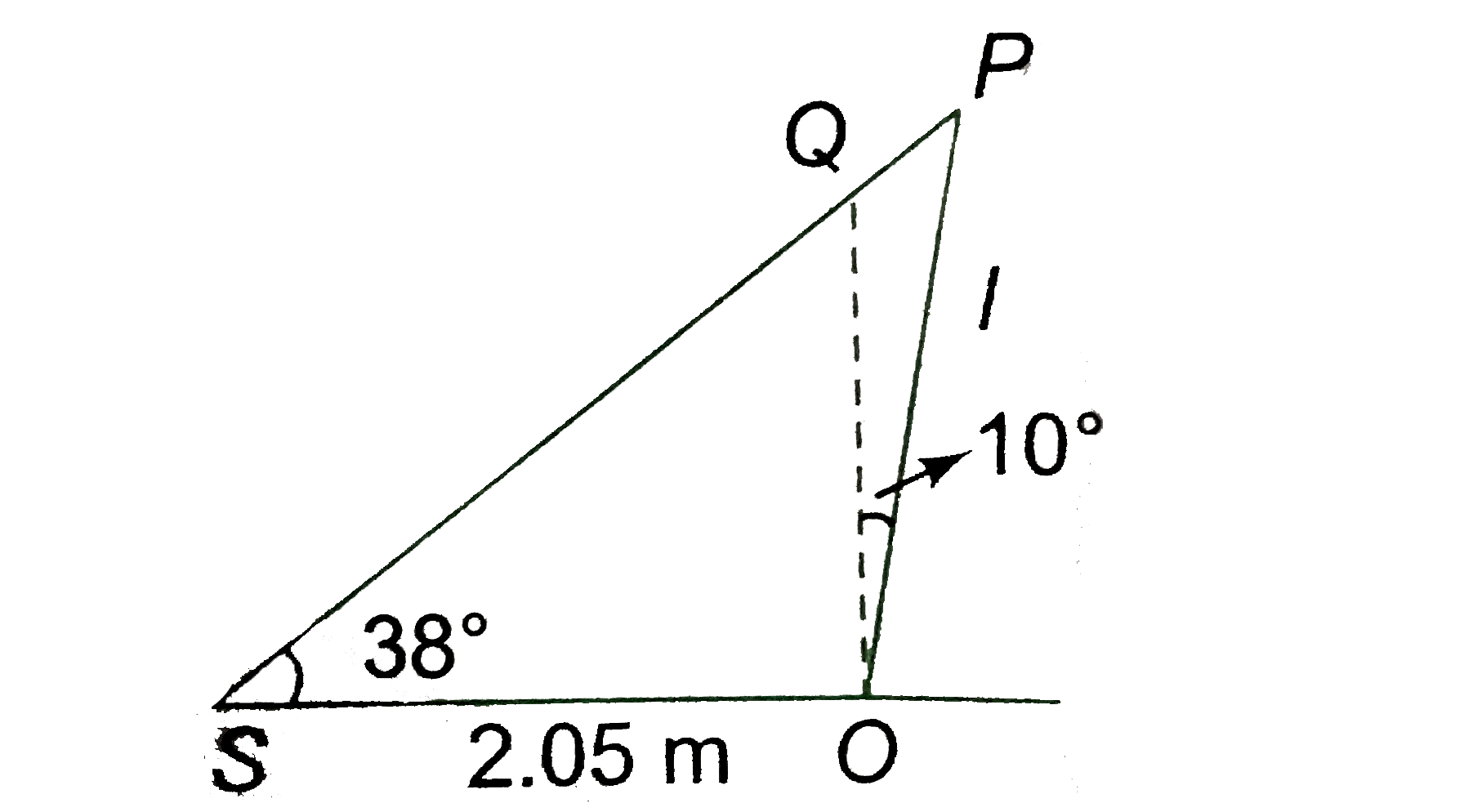
- The length of the shadow of a pole inclined at 10^@ to the vertical t...
Text Solution
|
- The length of the shadow of a pole inclined at 10^(@) to the vertical ...
Text Solution
|
- Find the angle of elevation of the sun (sun’s altitude) when the le...
Text Solution
|
- If the height of a pole is 2sqrt(3) metres and the length of its sh...
Text Solution
|
- The shadow of a pole is 9 m long when the angle of elevation of the su...
Text Solution
|
- The length of the shadow of a pole inclined at 10^(@) to the vertical ...
Text Solution
|
- The length of shadow of a pole is equal to the length of the pole, the...
Text Solution
|
- The length of the shadow of a pole inclined at 10^@ to the vertical t...
Text Solution
|
- Find the angle of elevation of the sun (sun’s altitude) when the le...
Text Solution
|