Similar Questions
Explore conceptually related problems
Recommended Questions
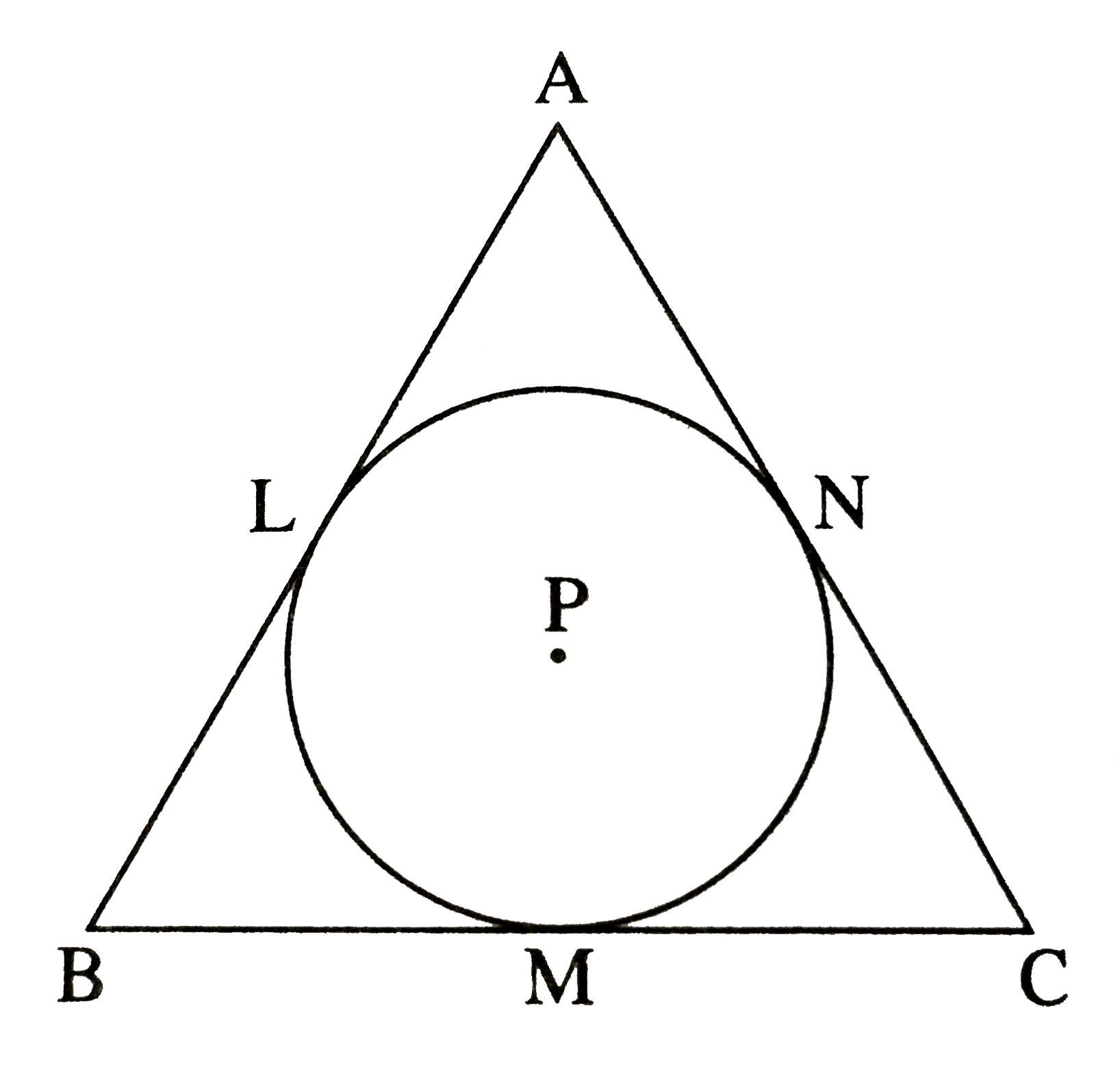
- A circle with centre P is inscribed in the triangle ABC. Side AB, side...
Text Solution
|
- The sides AB,BC and AC of a triangle ABC touch a circle with centre O ...
Text Solution
|
- A circle is touching the side BC of DeltaABC at P and touching AB and ...
Text Solution
|
- A circle is touching the side BC of a triangleABC at point P and touch...
Text Solution
|
- चित्र में एक वृत्त त्रिभुज ABC की भुजा BC को प पर स्पर्श ...
Text Solution
|
- A circle with centre P is inscribed in the Delta ABC Side AB, side BC...
Text Solution
|
- A circle with centre P is inscribed in the triangle ABC. Side AB, side...
Text Solution
|
- The radius of the circle touching two sides AB and AC of a triangle AB...
Text Solution
|
- In a right triangle ABC, a circle with a side. AB as diameter is draw...
Text Solution
|