Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT-QUADRILATERALS-EXERCISE 8.1
- If the diagonals of a parallelogram are equal, then it is a
Text Solution
|
- Show that if the diagonals of a quadrilateral bisect each other at ri...
Text Solution
|
- The angles of a quadrilateral are in the ratio 3\ :\ 5\ :\ 9\ :\ 13. F...
Text Solution
|
- Diagonal AC of a parallelogram ABCD bisects \ /A. Show that (i) it bi...
Text Solution
|
- ABCD is a rhombus. Show that diagonal AC bisects /Aas well as /Cand d...
Text Solution
|
- Show that the diagonals of a square are equal and bisect each other a...
Text Solution
|
- Show that if the diagonals of a quadrilateral are equal and bisect ea...
Text Solution
|
- ABCD is a rectangle in which diagonal AC bisects /Aas well as /C. Sho...
Text Solution
|
- In parallelogram ABCD, two points P and Q are taken on diagonal BD su...
Text Solution
|
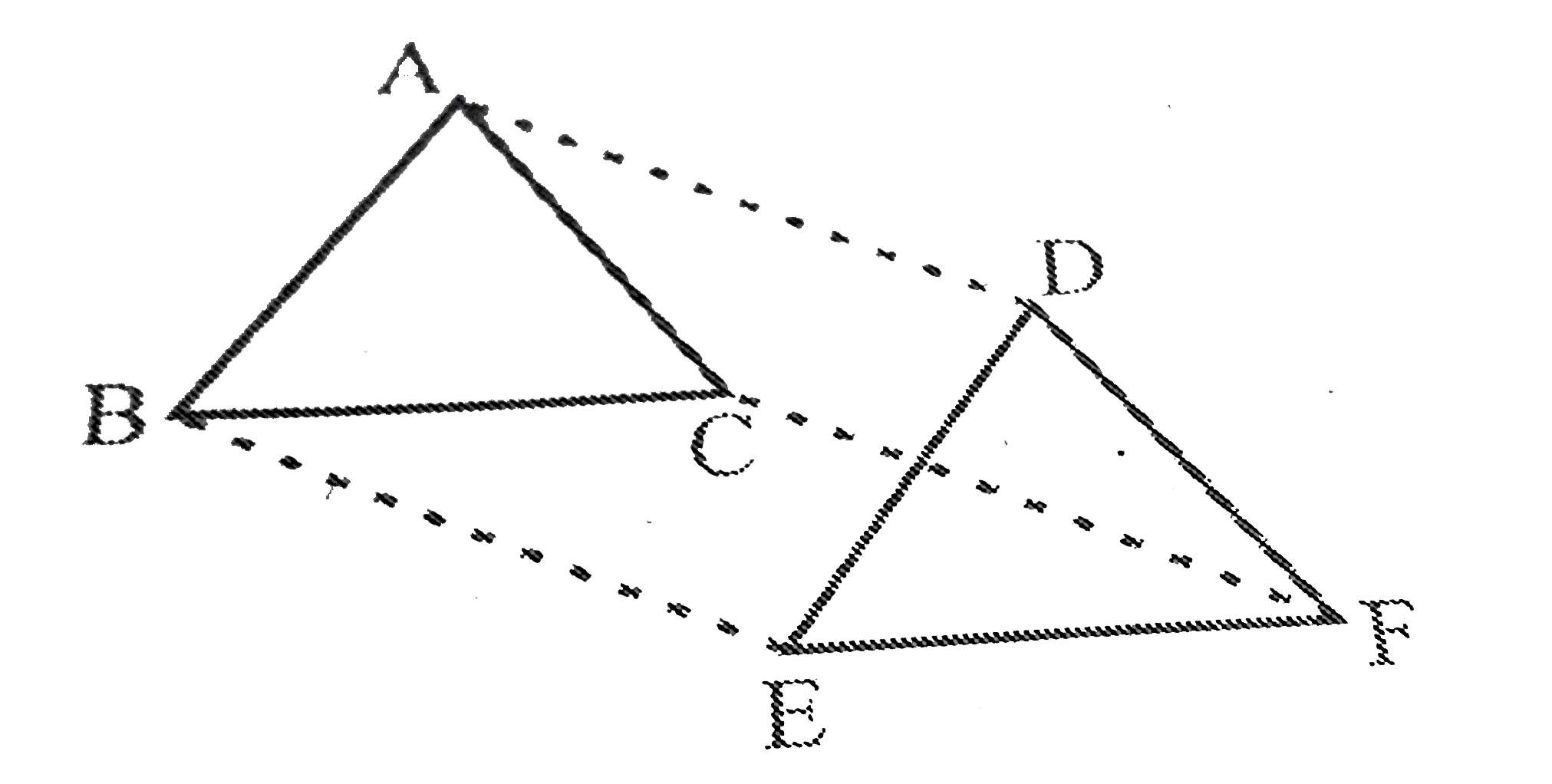
- In DeltaA B Cand DeltaD E F, A B\ =\ D E, A B\ ||\ D E, B C\ =\ E F an...
Text Solution
|
- ABCD is a parallelogram and AP and CQ are perpendiculars from vertice...
Text Solution
|
- ABCD is a trapezium in which AB||CD and AD=BC. Show that (i)/A=/B (i...
Text Solution
|