Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NCERT-QUADRILATERALS-SOLVED EXAMPLES
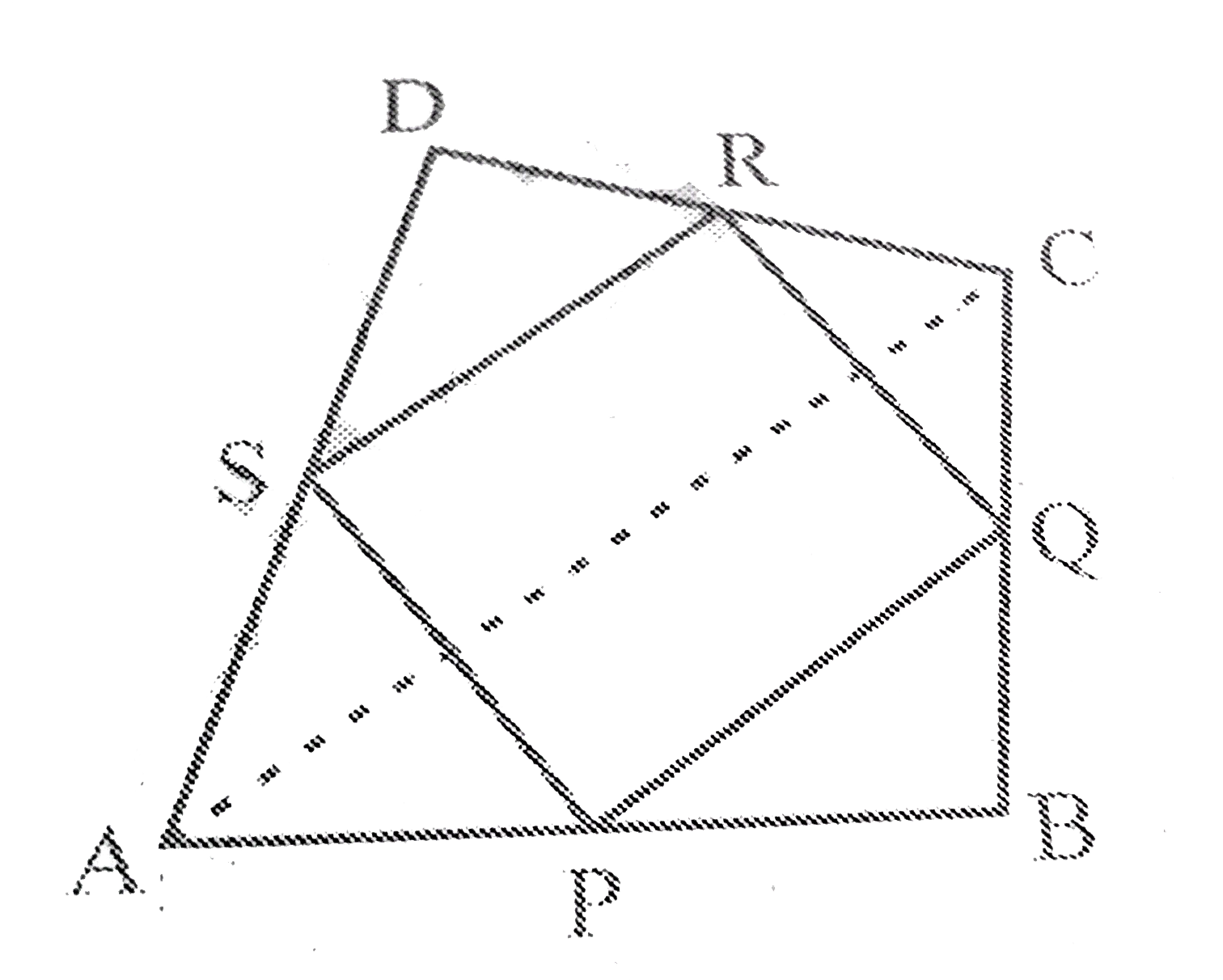
- ABCD is a quadrilateral in which P, Q, R and S are mid-points of the ...
Text Solution
|
- Show that each angle of a rectangle is a right angle.
Text Solution
|
- ABC is an isosceles triangle in which A B =A C. AD bisects exterior a...
Text Solution
|
- Show that the diagonals of a rhombus are perpendicular to each other
Text Solution
|
- Show that the bisectors of angles of a parallelogram form a rectangle...
Text Solution
|
- Two parallel lines l and m are intersected by a transversal p (see Fi...
Text Solution
|
- ABCD is a parallelogram in which P and Q are mid-points of opposite s...
Text Solution
|
- l, m and n are three parallel lines intersected by transversals p and...
Text Solution
|
- In DeltaA B C, D, E and F are respectively the mid-points of sides AB...
Text Solution
|