Text Solution
Verified by Experts
Topper's Solved these Questions
TRIANGLES
NAGEEN PRAKASHAN|Exercise Problems From NCERT/ Exemplar|14 VideosTRIANGLES
NAGEEN PRAKASHAN|Exercise Exercise 6a|23 VideosSTATISTICS
NAGEEN PRAKASHAN|Exercise Revision Exercise Long Answer Questions|5 VideosVOLUME AND SURFACE AREA OF SOLIDS
NAGEEN PRAKASHAN|Exercise Revisions Exercise Long Answer Questions|5 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN-TRIANGLES -Revision Exercise Long Questions
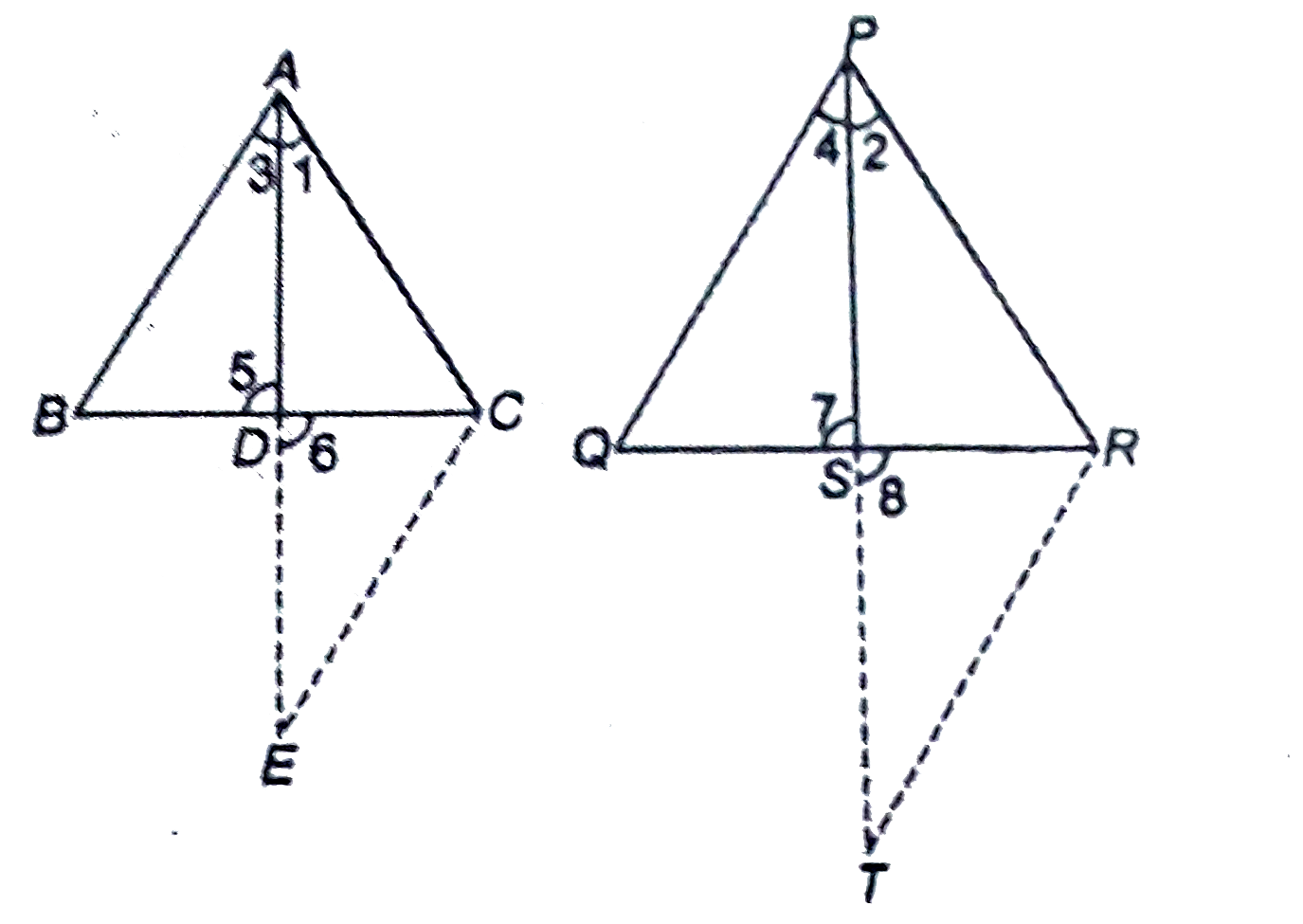
- If two sides and a median bisecting the third side of a triangle ar re...
Text Solution
|
- The bisector of interior angleA of triangleABC meets BC in D, and the ...
Text Solution
|
- AD is a median of triangleABC. The bisectors of angleADB and angleADC ...
Text Solution
|
- triangleABC and triangleDBC are two triangles on the same base BC. A a...
Text Solution
|
- Prove that three times the sum of the squares on the sides of a triang...
Text Solution
|