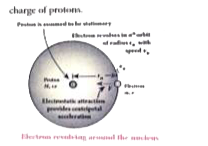
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Derive the energy expression for hydrogen atom using Bohr atom model.
Text Solution
|
- In Bohr's model of hydrogen atom ,
Text Solution
|
- which of the following postulates of the Bohr model led to the quantiz...
Text Solution
|
- Using Rutherford model of atom , derive the expression for the total ...
Text Solution
|
- Derive the energy expression for hydrogen atom using Bohr atom model.
Text Solution
|
- Using Rutherford model of atom, derive an expression for the total ene...
Text Solution
|
- Derive the energy expression for hydrogen atom using Bohr atom model.
Text Solution
|
- Derive the energy expression for hydrogen atom using Bohr atom model.
Text Solution
|
- Using Bohr's atomic model, derive the expression for the radius of nth...
Text Solution
|