(i) When an electric current passing through a coil changes with time, an emf is induced in the neighbouring coil. This phenomenon is known as mutual induction and the emf is called mutually induced emf.
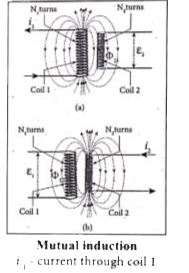
(ii) Consider two coils which are placed close to each other. If an electric current il is sent through coil 1, the magnetic field produced by it is also linked with coil 2 as shown in Figure (a).
(iii) `M_(21)`, is the mutual inductance of the coil 2 with respect to coil 1. It is also called as coefficient of mutual induction. If `i_1 = 1A`, then `M_(21) = N_(2)phi_(21)`.
(iv). Therefore, the mutual inductance M,, is defined as the flux linkage of the coil 2 when 1A current flows through coil 1.
(v) When the current `i_1`, changes with time, an emf `epsi_(2)`, is induced in coil 2. From Faraday.s. law of electromagnetic induction, this mutually induced emf `epsi_(2)`, is given by
`epsi_(2)= -(d(N_(2)phi_(21)))/(dt)= -(d(M_(21)i_(1)))/(dt)`
`epsi_(2)=-M_(21) (di_(1))/(dt)`
(or) `M_(21) = (-epsi_(2))/((di_1)/(dt))`
(vi) The negative sign shows that the mutually induced emf always opposes the change in current `i_(1)`, with respect to time. If `(di_(i))/(dt) =1`
`As^(-1)`, then `M_(21) = - epsi_(2)`.
(vii) Mutual inductance `M_(21)`, is also defined as the opposing emf induced in the coil 2 when the rate of change of current through the coil 1 is 1`As^(-1)`.
(viii) Similarly, if an electric current `i_2`, through coil 2 changes with time, then emf `ę_1`, is induced in coil 1. Therefore,
`M_(12)=(N_(1)phi_(12))/i_(2)"and "M_(12)= (-epsi_(1))/((di_(2))/(dt))`
where `M_(12)` is the mutual inductance of the coil 1 with respect to coil 2. It can be shown that for a given pair of coils, the mutual inductance is same.
i.e., `M_(21) = M_(12) = M`
(ix) In general, the mutual induction between two coils depends on size, shape, the number of turns of the coils, their relative orientation and permeability of the medium.
