Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
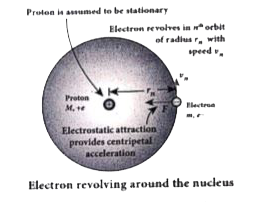
- Derive the expression for the radius of the orbit of the electron and ...
Text Solution
|
- बोर मॉडल के अनुसार हाइड्रोजन परमाणु की n वीं कक्षा में इलेक्ट्रॉन के व...
Text Solution
|
- Using Bohr's postulates of the atomic model, derive the expression fo...
Text Solution
|
- Derive the energy expression for hydrogen atom using Bohr atom model.
Text Solution
|
- Derive the expression for the radius of the orbit of the electron and ...
Text Solution
|
- Derive the energy expression for hydrogen atom using Bohr atom model.
Text Solution
|
- Derive the expression for the radius of the orbit of the electron and ...
Text Solution
|
- Derive the energy expression for hydrogen atom using Bohr atom model.
Text Solution
|
- Using Bohr's atomic model, derive the expression for the radius of nth...
Text Solution
|