(i) AB be the electric dipole ( -q at A tna +q at B).
2a be the distance between -q and +q.
.r. be the distance between the point .p. and mid point .O. of AB.
`.theta.` be the angle between OP and OB.
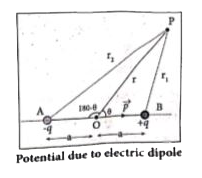
(ii) Let `r_1` be the distance of point P from +q and `r_2` be the distance of point P from -q.
Potential at P due to charge +q `= 1/(4 pi epsi_0)q/r_1`
Potential at P due to charge -q `=-1/(4piepsi_(0))q/r_2`
Total potential at the point p,
`V = 1/(4 pi epsi_0 ) q (1/r_1 - 1/r_2)" ....(1)"`
(iii) By the cosine law for triangle BOP.
`r_1^2 = r^2 +a^2 - 2ra costheta`
`r_1^2 = r^2 (1+a^2/r^2 - (2a)/r cos theta)`
Since a a`ltlt`r, term `a^2/r^2` is very small and can be neglected. Therefore
`r_1^2=r^2 (1-2a(cos theta)/r)`
(or) `r_1 = r(1-(2a)/rcos theta)^(1/2)`
`1/r_1 =1/r (1-(2a)/r cos theta)^(1/2)`
(iv) Using binamial theorem we get.
`1/r_1 = 1/r (1+a/rcostheta)" ...(2)"`
Similarly applying the cosne law for triangle AOP,
`r_2^2 = r^2 -a^2-2racos (180 - theta)`
Since cos (`180 - theta`) = `-cos theta` we get
`r_2^2 = r^2 + a^2 + 2ra cos theta`
Neglecting `a^2/r^2` ( because `r gt gt a` )
`a_2^2 = r^2(1+(2a cos theta)/r)`
`r_2 = r(1+(2a cos theta)/r)^(1/2)`
Using Binomial theorem we get
`1/r_2 = 1/r (1-a (cos theta)/r)" ...(3)"`
Substituting equation (3) and (2) in equation (1),
`V=1/(4piepsi_(0))q(1/r(1+a(cos theta)/r)-1/r (1-a(cos theta)/r))`
`V = q/(4piepsi_(0))(1/r(1+a(costheta)/r)-1/r (1-a(cos theta)/r))`
`V=1/(4 piepsi_(0))(2aq)/r^2 cos theta`
(v) But the electric dipole moment p = 2qa and we get,
`V = 1/(4pi epsi_0)((pcos theta)/r^2)`
If p `cos theta = vec p * hatr,` where `hatr` is the unit vector from the point O to point P. then
`V = 1/(4piepsi_0)(vecp*hatr)/r^2" "(r gtgta)" ...(4)"`
Spacial cases
Case (i) If the point P lies on the axial line then `theta = 0`, then
`v = 1/(4 pi epsi_(0)) p/r^2 " ...(5)"`
Case (ii) If the point P lien on the axial line then `theta = 180^@`, then
`V = 1/ (4 pi epsi_(0)) p/r^2 " ...(6)"`
Case (iii) If the point P lies on the equatorial line, then `theta = 90^@`. Hence
V = 0 ...(7)
