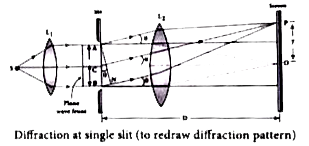
(i) Let a parallel beam of light fall normally on a single slit AB of width. The diffracted beam falls on a screen kept at a distance. The center of the slit is G.
(ii) A straight line through C perpendicular ll to the plane of slit meets the center of the screen at O. The intensity at any point P on the screen is to be found.
(iii) The lines joining P to the different points on the slit can be treated as parallel lines, making an angle 8 with the normal CO.
(iv) All the waves start parallel to each other. from different points of the slit and interfere at point P and other points to give the resultant intensities.
(v) The point P is in the geometrically shadowed region, up to which the central maximum is spread due to diffraction. Condition for the point P to be of various minima.
(vi) Divide the slit into much smaller even number of parts. Then, add their contributions at P with the proper path difference to show that destructive interference takes place at that point to make it minimum.
Condition for P to be first minimum :
(i) Let us divide the slit AB into two half.s AC and CB. Now the width of AC is`(a/2)`. We have different points on the slit which are separated by the same width (here `a/2`) called corresponding points as shown in Figure.
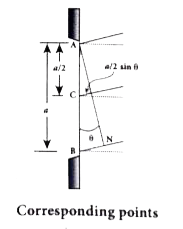
(ii) The path difference of light waves from different corresponding points meeting at point P and interfere destructively to make it first minimum. The path difference `delta` between waves from these corresponding points is, `delta = a/2 sin theta`
The condition for P to be first minium,
`a/2 sin theta = lamda/2`
`a sin theta = lamda ` ( first minimum )
Condition for P to be second minimum : (i) Let us divide the slit AB into four equal parts. Now, the width of each part is `a/4` We have several corresponding points on the slit which are separated by the same width `a/4`. The path difference 8 between waves from these corresponding points is, `delta = a/4 sin theta`.
`a sin theta = 2 lamda` ( second minimum )
Condition for P to be `n^(th)` order minimum : The same way the slit is divided in to six equal parts to explain the condition for P to be third minimum is, `a/(2n)sin theta lamda/2`
`a sin theta = n lamda `(`n^(th)` minium )

