Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
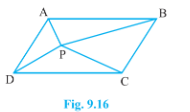
- In Fig. 9.16, P is a point in the interior of a parallelogram ABCD. S...
Text Solution
|
- Diagonals AC and BD of a quadrilateral ABCD intersect each other at P...
Text Solution
|
- In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q...
Text Solution
|
- In Fig.9.29, a r\ (B D P)\ =\ a r\ (A R C)and a r\ (B D P)\ =\ a r\ (A...
Text Solution
|
- Prove that the figure formed by joining the mid-points of the pair of ...
Text Solution
|
- In Figure, P is a point in the interior of a parallelogram A B C D . S...
Text Solution
|
- In Figure, A B C D\ a n d\ P Q R C are rectangles and Q is the mid-poi...
Text Solution
|
- In Figure, P is a point in the interior of a parallelogram A B C Ddo...
Text Solution
|
- Diagonals A C and B D of a quadrilateral A B C D intersect each a...
Text Solution
|