Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
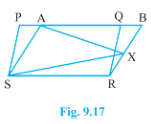
- In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on ...
Text Solution
|
- ABCD is a quadrilateral in which P, Q, R and S are mid-points of the ...
Text Solution
|
- In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on ...
Text Solution
|
- Prove that the figure formed by joining the mid-points of the pair of ...
Text Solution
|
- In Figure, P Q R S and A B R S are parallelograms and X is any point o...
Text Solution
|
- P Q R S is a trapezium having PS a n d Q R as parallel sides. A is a...
Text Solution
|
- Show that for all values of p, q, r, s the matrices, P=[(p,q),(-q,p...
Text Solution
|
- if P,q, r, s in R such that p r= 2 ( q+ s) then
Text Solution
|
- IF P,Q,R and S are respectively the mid-points of the sides of a para...
Text Solution
|