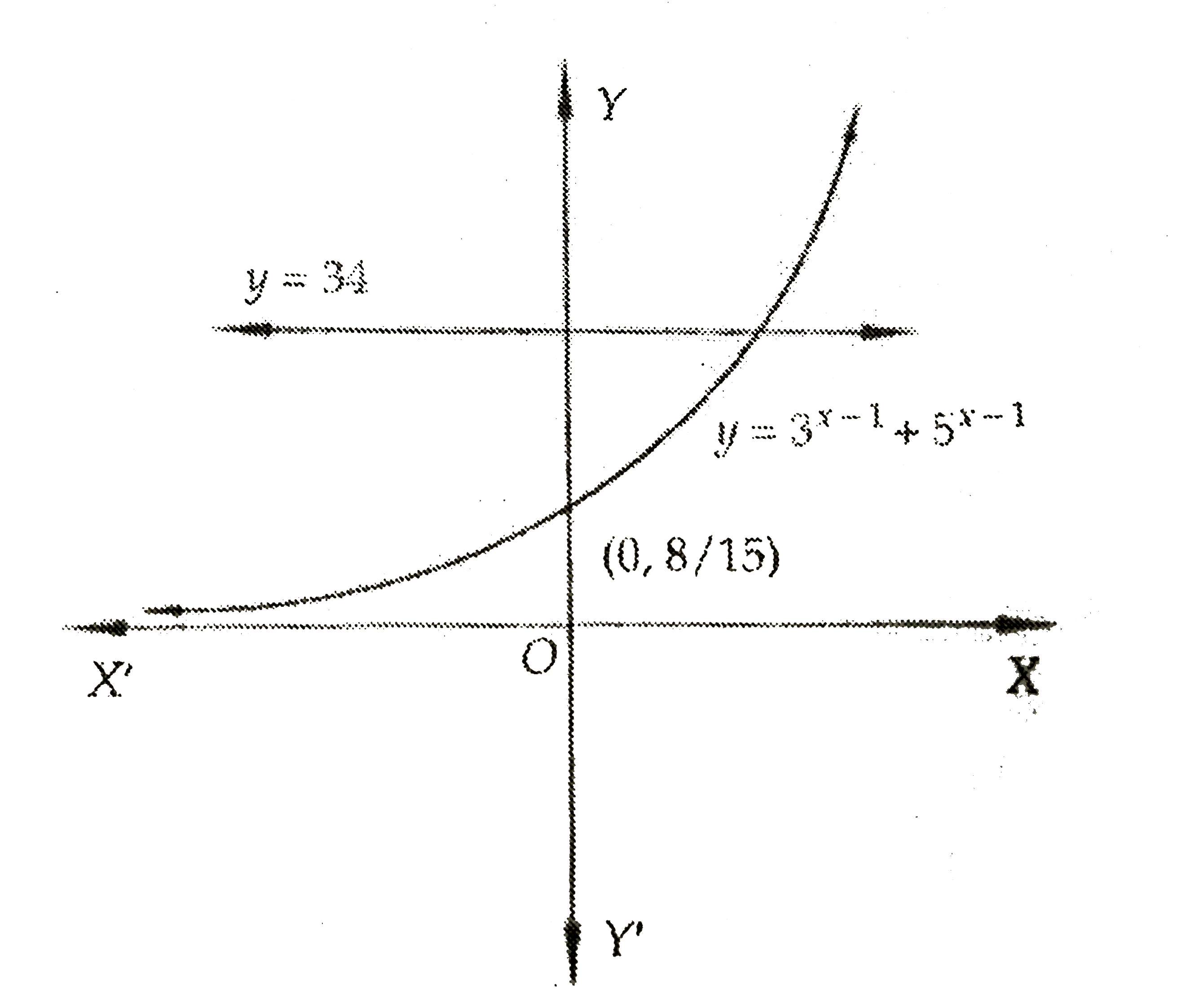
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- The equation sin^-1x-cos^-1x=cos^-1(sqrt3/2) has
Text Solution
|
- If y=(a^(cos^-1x))/(1+a^(cos^-1x))andz=a^(cos^-1x),then (dy)/(dx)=
Text Solution
|
- প্রমাণ করো যে, sin^-1cossin^-1x+cos^-1sincos^-1x=pi/2
Text Solution
|
- প্রমাণ করো:{cos(sin^-1x)}^2={sin(cos^-1x)}^2
Text Solution
|
- সমাধান করো:sin^-1x+sin^-1(1-x)=cos^-1x
Text Solution
|
- f(x) = sin (sin^-1x + cos^-1x) (absxle1) অপেক্ষকের প্রসার বা পাল্লা (r...
Text Solution
|
- সমাধান করো:sin^-1x-cos^-1x=sin^-1(3x-2)
Text Solution
|
- সমাধান করো:cos^-1x-sin^-1x=cos^-1(xsqrt3)
Text Solution
|
- cos^-1x>sin^-1x எனில்,
Text Solution
|