Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
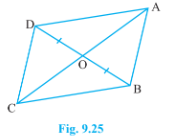
- In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at ...
Text Solution
|
- In Fig. 9.25, diagonals AC and BD of quadrilateral ABCD intersect at ...
Text Solution
|
- If the diagonals A C ,B D of a quadrilateral A B C D , intersect at O ...
Text Solution
|
- Show that the diagonals of a parallelogram divide it into four trian...
Text Solution
|
- Diagonals A C and B D of a quadrilateral A B C D intersect at O in suc...
Text Solution
|
- A B C D is a trapezium in which A B C D . The diagonals A C and...
Text Solution
|
- Diagonals A C\ a n d\ B D of a quadrilateral A B C D intersect a...
Text Solution
|
- A B C D IS A PARALLELOGRAM AND O is any point in its interior. Prov...
Text Solution
|
- A B C D is a parallelogram whose diagonals intersect at Odot If P i...
Text Solution
|