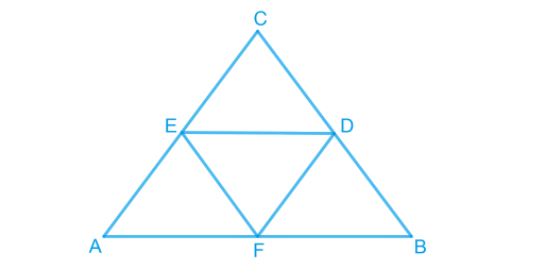
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- D, E and F are respectively the mid-points of the sides BC, CA and AB...
Text Solution
|
- In DeltaA B C, D, E and F are respectively the mid-points of sides AB...
Text Solution
|
- D, E and F are respectively the mid-points of the sides BC, CA and AB...
Text Solution
|
- In a parallelogram A B C D ,E ,F are any two points on the sides A B a...
Text Solution
|
- E , F , G , H are respectively, the mid-points of the sides A B ,B C ,...
Text Solution
|
- D,E and F are respectively the mid-points of the sides BC,CA and AB of...
Text Solution
|
- A B C D is a parallelogram, G is the point on A B such that A G=2 ...
Text Solution
|
- If E ,F ,G and H are respectively the mid-points of the sides of a p...
Text Solution
|
- In DeltaA B C, D, E and F are respectively the mid-points of sides AB...
Text Solution
|