Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
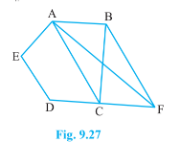
- In Figure, A B C D E\ is a pentagon. A line through B parallel to A...
Text Solution
|
- In Figure, A B C D E is a pentagon. A line through B parallel to A C m...
Text Solution
|
- If A B C and D E F are two triangles such that (A B)/(D E)=(B C)/...
Text Solution
|
- In Figure, A B C D E\ is a pentagon. A line through B parallel to A...
Text Solution
|
- Any point D is taken in the base B C of a triangle A B C\ a n d\...
Text Solution
|
- In Figure, A B C D ,\ A B F E\ a n d\ C D E F are parallelograms. Prov...
Text Solution
|
- A B C D is a parallelogram in which B C is produced to E such th...
Text Solution
|
- In Figure D and E are two points on BC such that BD=DE=EC Show that ar...
Text Solution
|
- A B C D is a parallelogram. A D is a produced to E so that D E=D C and...
Text Solution
|