Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-TRIGONOMETRIC FUNCTIONS -SINGLE CORRECT ANSWER TYPE
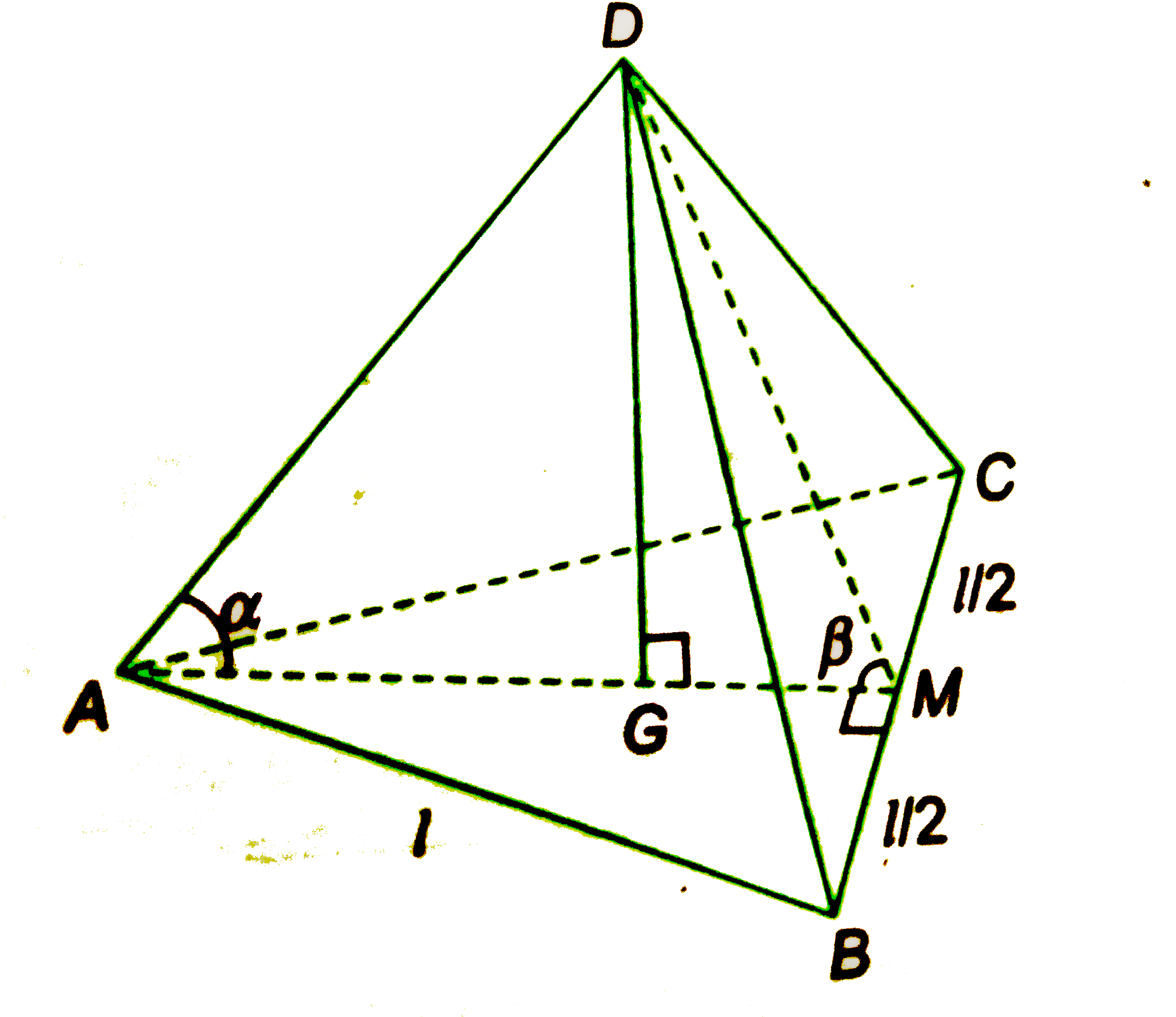
- find the height of the regular pyramid with each edge measuring l cm. ...
Text Solution
|
- The circular wire of diameter 10 cm is cut and placed along the circum...
Text Solution
|
- sintheta/(1-cottheta)+costheta/(1-tantheta)= (a)theta (b)1 (c)costh...
Text Solution
|
- If theta in (pi//4, pi//2) and sum(n=1)^(oo)(1)/(tan^(n)theta)=sin the...
Text Solution
|
- The value of (tan^(2)20^(@)-sin^(2)20^(@))/(tan^(2)20^(@).sin^(2)20^(@...
Text Solution
|
- If 15 sin^(4)alpha+10cos^(4)alpha=6, then the value of 8 cosec^(6)alph...
Text Solution
|
- In DeltaABC, if sin A + sin B + sin C= 1 + sqrt2 and cos A+cos B+cos...
Text Solution
|
- If (sin^(2)x-2cos^(2)x+1)/(sin^(2)x+2cos^(2)x-1)=4, then the value of ...
Text Solution
|
- If sintheta,tantheta,costheta are in G.P. then 4sin^2theta-3sin^4theta...
Text Solution
|
- If tantheta-cottheta=aandsintheta+costheta=b(b^2-1)^2(a^2+4) is equal...
Text Solution
|
- The least value of 18 sin^(2)theta+2 cosec^(2)theta-3 is
Text Solution
|
- If tan^2 alpha tan^2 beta + tan^2 beta tan^2 gamma + tan^2 gamma tan^2...
Text Solution
|
- If x,y,z be all positive acute angles then the least value of tanx(cot...
Text Solution
|
- Three circles each of radius 1, touch one another externally and they ...
Text Solution
|
- If (cos alpha)/(cos A)+(sin alpha)/(sin A)+(sin beta)/(sin A)=1, where...
Text Solution
|
- Consider angles alpha = (2n+(1)/(2))pi pm A and beta = m pi +(-1)^(m)(...
Text Solution
|
- Which of the following is true ?
Text Solution
|
- If the angle A of a triangle ABC is given by the equation 5 cos A + 3 ...
Text Solution
|
- Which of the following is greatest ?
Text Solution
|
- The number of value/values of x for which sin y=x^(2)-2x si possible i...
Text Solution
|
- Which of the following is not correct ?
Text Solution
|