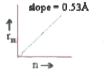
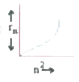A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
STRUCTURE OF ATOM
NARAYNA|Exercise EXERCISE - I (H. W.) dE-BROGLIE.S & HEISENBERG.S|2 VideosSTRUCTURE OF ATOM
NARAYNA|Exercise EXERCISE - I (H. W.) QUANTUM MECHANICAL MODEL OF ATOM|6 VideosSTRUCTURE OF ATOM
NARAYNA|Exercise EXERCISE - I (H. W.) H-SPECTRUM|5 VideosSTATES OF MATTER
NARAYNA|Exercise A & R TYPE QUESTIONS|16 VideosTHERMODYNAMICS
NARAYNA|Exercise Assertion- Reason|5 Videos
Similar Questions
Explore conceptually related problems
NARAYNA-STRUCTURE OF ATOM-EXERCISE - I (H. W.) BOHR.S ATOMIC MODEL
- With increasing atomic number of a single electron species, the energy...
Text Solution
|
- The ratio of the radius of the Bohr orbit for the electron orbiting th...
Text Solution
|
- Which of the following curves may represent the radius of orbit (rn) i...
Text Solution
|
- How much energy is required to ionise a H atom if the electron occupie...
Text Solution
|
- If the speed of electron in the first bohr orbit of hydrogen atom is x...
Text Solution
|