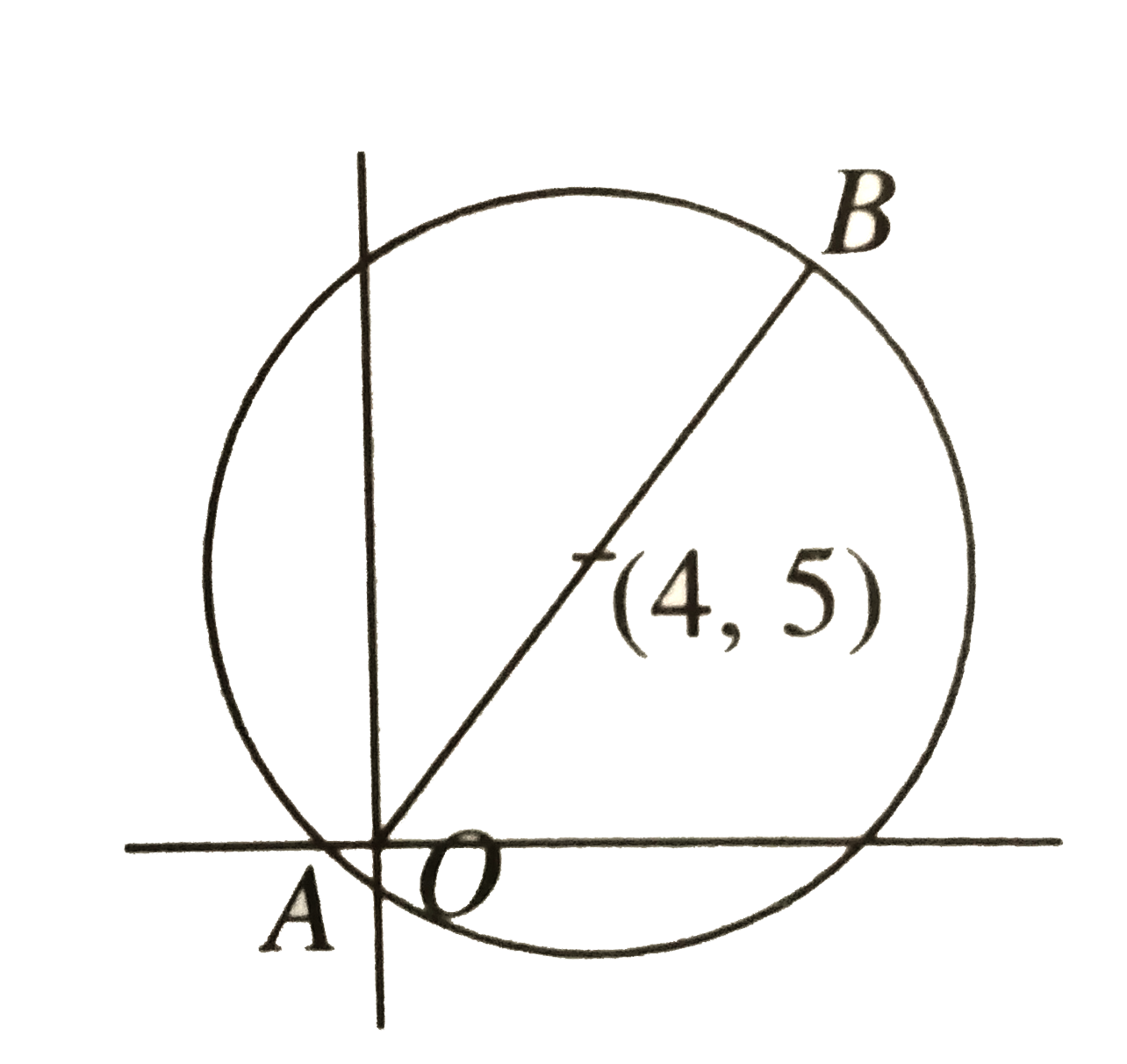
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-COMPLEX NUMBERS-Comprehension
- Consider the region R in the Argand plane described by the complex num...
Text Solution
|
- Consider the region R in the Argand plane described by the complex num...
Text Solution
|
- Consider the region R in the Argand plane described by the complex num...
Text Solution
|
- Let z(1) and z(2) be complex numbers such that z(1)^(2)-4z(2)=16+20i a...
Text Solution
|
- Let z(1) and z(2) be complex numbers such that z(1)^(2)-4z(2)=16+20i a...
Text Solution
|
- Let z(1) and z(2) be complex numbers such that z(1)^(2)-4z(2)=16+20i a...
Text Solution
|
- The locus of any point P(z) on argand plane is arg((z-5i)/(z+5i))=(pi)...
Text Solution
|
- The locus of any point P(z) on argand plane is arg((z-5i)/(z+5i))=(pi)...
Text Solution
|
- The locus of any point P(z) on argand plane is arg((z-5i)/(z+5i))=(pi)...
Text Solution
|
- A person walks 2sqrt(2) units away from origin in south west direction...
Text Solution
|
- A person walks 2sqrt(2) units away from origin in south west direction...
Text Solution
|