Similar Questions
Explore conceptually related problems
Recommended Questions
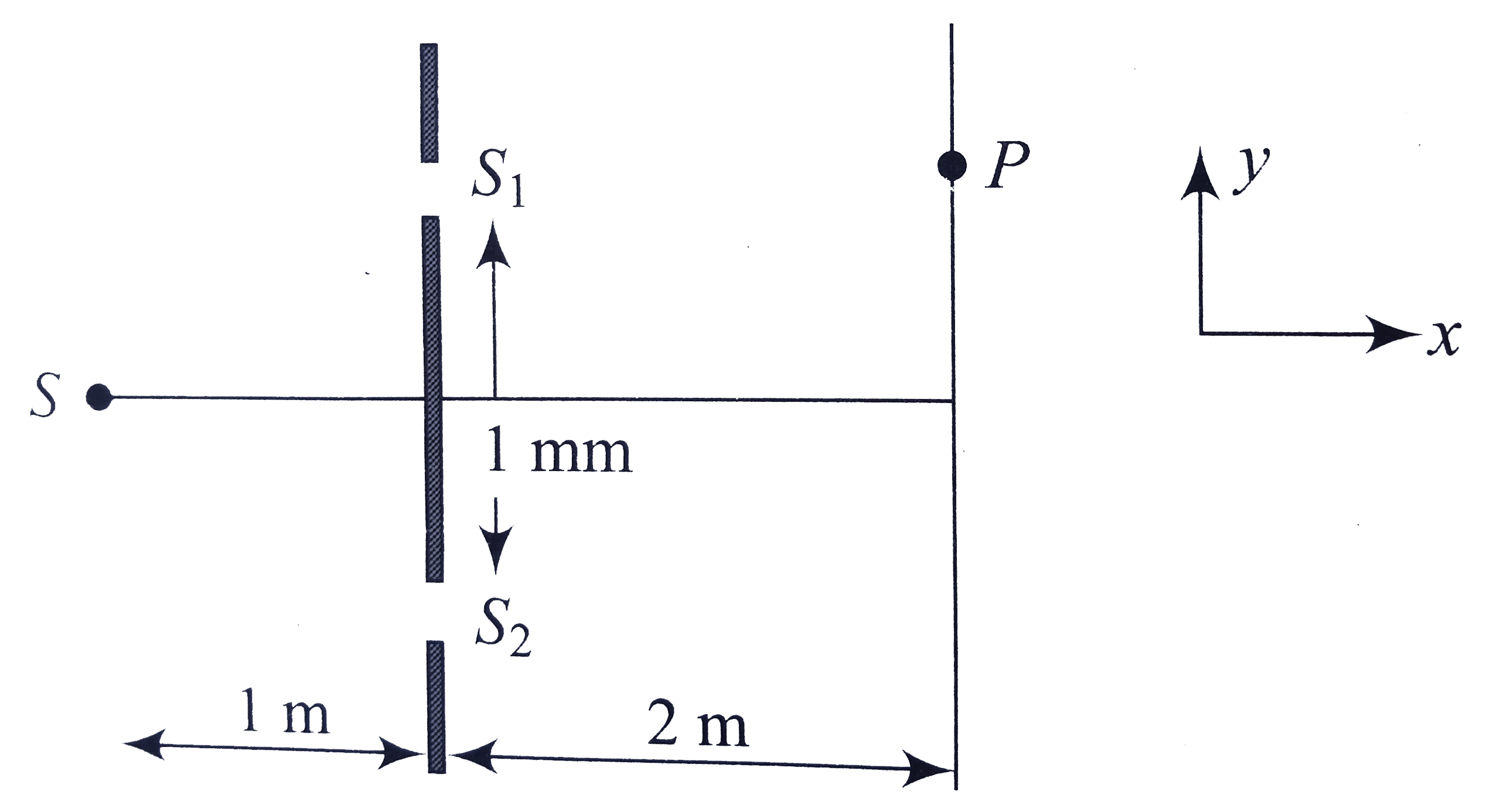
- In young's double-slit experiment set up, sources S of wavelength 50 n...
Text Solution
|
- In young's double-slit experiment set up, sources S of wavelength 50 n...
Text Solution
|
- In a Young's double-slit experiment set up, source S of wavelength 600...
Text Solution
|
- In a Young's double-slit experiment set up, source S of wavelength 600...
Text Solution
|
- In a Young's double-slit experiment set up, source S of wavelength 600...
Text Solution
|
- Find the ratio of intensities at the two points X and Y on a screen in...
Text Solution
|
- In a modified YDSE the sources S of wavelength 5000 A oscillates about...
Text Solution
|
- Figure shows a Young's double slit experiment set-up. The source S of ...
Text Solution
|
- In a Young's double slit experiment set up, source S of wavelength 500...
Text Solution
|