Similar Questions
Explore conceptually related problems
Recommended Questions
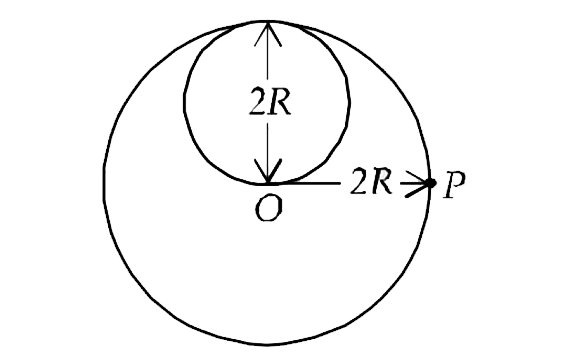
- A lamina is made by removing a small disc of diameter 2R from a bigg...
Text Solution
|
- A lamina is made by removing a small disc of diameter 2R from a bigg...
Text Solution
|
- From a thin uniform disc of radius 2R. Another disc of diameter 2R is ...
Text Solution
|
- A lamina is made by removing a small disc of diameter 2 R from a bigge...
Text Solution
|
- Find the position of center of mass of the uniform lamina shown in fig...
Text Solution
|
- Mass of bigger disc having radius 2R is M. A disc of radius R is cut f...
Text Solution
|
- From a circular disc of radius R and mass 9M, a small disc of radius R...
Text Solution
|
- Find the position of centre of mass of the uniform lamina shown in fig...
Text Solution
|
- A uniform disc having radius 2R and mass density sigma as shown in fig...
Text Solution
|