Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
GEOMETRY
FULL MARKS|Exercise Assignment (I. Choose the correct answer)|5 VideosGEOMETRY
FULL MARKS|Exercise Assignment (II Match the following)|1 VideosGEOMETRY
FULL MARKS|Exercise Additional Questions I. Multiple Choice Question.|20 VideosCOORDINATE GEOMETRY
FULL MARKS|Exercise TEXTBOOK ACTIVITY|2 VideosMENSURATION
FULL MARKS|Exercise Assignment (II. Answer the following questions)|8 Videos
Similar Questions
Explore conceptually related problems
FULL MARKS-GEOMETRY-Additional Questions II. Answer the following questions
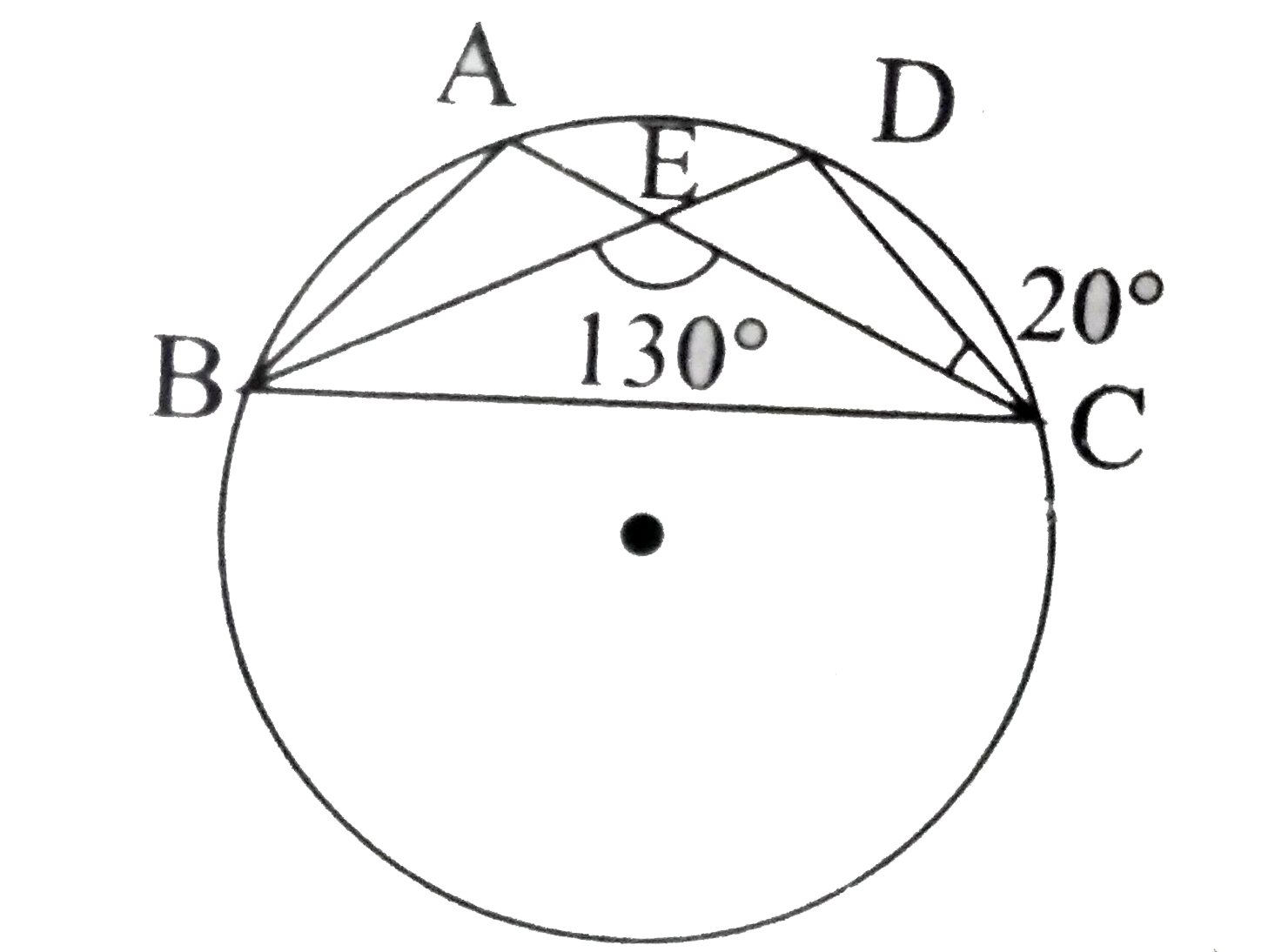
- In the figure find x^(@) and y^(@)
Text Solution
|
- The angles of quadrilateral are in the ratio 3:5:9:13. Find the angles...
Text Solution
|
- Diagonal AC of a parallelogram ABCD bisects angleA. Show that (i) it...
Text Solution
|
- ABCD is a parallelogram and AP and CQ are perpendiculars from vertex A...
Text Solution
|
- ABCD is a rectangle and P,R and S are the mid - points of the AB, BC, ...
Text Solution
|
- In the figure A,B and C are three points on a circle with centre O suc...
Text Solution
|
- In the given figure A,B,C and D are four points on a circle, AC and BD...
Text Solution
|
- In the given figure KLMN is a cyclic quadrilateral. KD is the tangent ...
Text Solution
|
- In the given figure angle PQR=100^(@), where P,Q and R are points on a...
Text Solution
|
- AB and CD are two parallel chords of a circle which are on opposite s...
Text Solution
|