Home
Class 9
MATHS
If sintheta=(a)/(sqrt(a^(2)+b^(2))) then...

If `sintheta=(a)/(sqrt(a^(2)+b^(2)))` then show that b sin `theta` = a cos `theta`.

Text Solution

Verified by Experts

The correct Answer is:
Hence, PROVED.
Promotional Banner

Topper's Solved these Questions

  • TRIGONOMETRY

    FULL MARKS|Exercise EXERCISE - 6.2|4 Videos

  • TRIGONOMETRY

    FULL MARKS|Exercise EXERCISE - 6.3|1 Videos

  • STATISTICS

    FULL MARKS|Exercise Assignment (Answer the following question)|10 Videos

Similar Questions

Explore conceptually related problems

If cos theta+sin theta=sqrt2 cos theta, show that cos theta-sin theta=sqrt2 sin theta .

Solve the equations: sin theta + cos theta = sqrt(2)

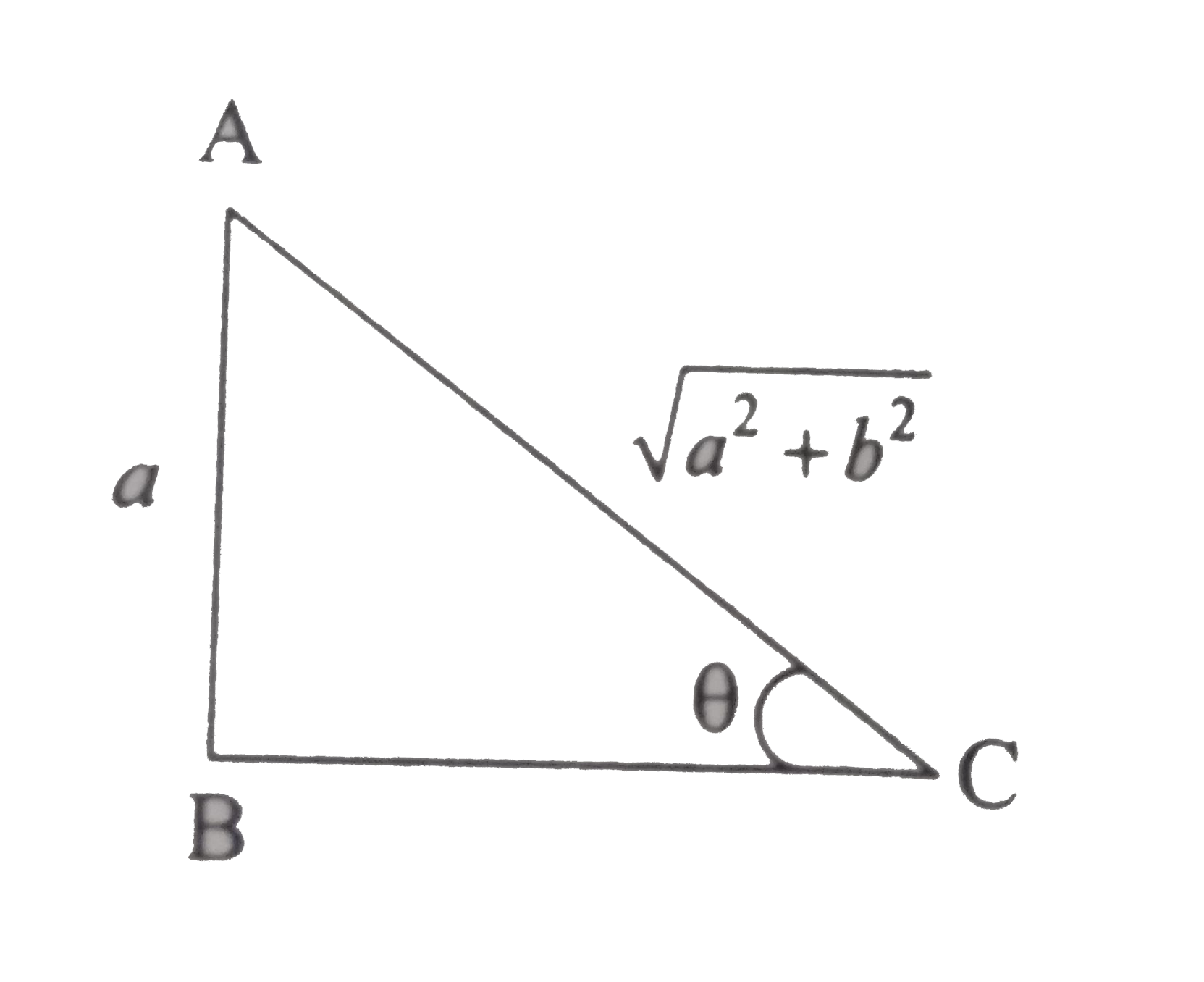
If theta=3alpha and sintheta=a/(sqrt(a^2+b^2)), the value of the expression acos e calpha-bsecalpha is (a) a/(sqrt(a^2+b^2)) (b) 2sqrt(a^2+b^2) (c) a+b (d) none of these

If a cos theta - b sin theta = c, show that a sin theta + b cos theta = pm sqrt(a^(2) + b^(2) - c^(2))

Solve sqrt(3) cos theta-3 sin theta =4 sin 2 theta cos 3 theta .

If tan theta = 1/b , then ( a sin theta - b cos theta )/( a sin theta + b cos theta) is

Prove that the product of the lengths of the perpendiculars drawn from the points (sqrt(a^(2) - b^(2)) , 0) " and " (- sqrt(a^(2) - b^(2)), 0) to the line x/a cos theta + y/b sin theta = 1 " is " b^(2) .

Show that the equation of the normal to the curve x=a cos ^(3) theta, y=a sin ^(3) theta at 'theta ' is x cos theta -y sin theta =a cos 2 theta .

If cos theta+sin theta=sqrt(2)cos theta then prove that cos theta-sin theta=sqrt(2)sin theta