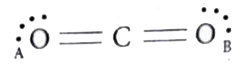A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
CHEMICAL BONDING
FULL MARKS|Exercise TEXTUAL EVALUATION SOLVED (SHORT ANSWER QUESTIONS.)|25 VideosCHEMICAL BONDING
FULL MARKS|Exercise IN TEXT QUESTION-EVALUATE YOURSELF|10 VideosBASIC CONCEPTS OF ORGANIC REACTIONS
FULL MARKS|Exercise Additional Questions Solved (5-Marks Question)|10 VideosENVIRONMENTAL CHEMISTRY
FULL MARKS|Exercise ADDITIONAL QUESTIONS SOLVED ( 5-Mark Questions )|8 Videos
Similar Questions
Explore conceptually related problems
FULL MARKS-CHEMICAL BONDING -ADDITIONAL QUESTIONS SOLVED (5-MARK QUESTIONS)
- In the molecule O(A) = C = O(B), the formal charge on O(A)C " and " O...
Text Solution
|
- Explain about Kossel-Lewis approach to chemical bonding.
Text Solution
|
- (i) What is meant by covalent bond? (ii) Explain the covalent bondin...
Text Solution
|
- (i) What is an ionic bond? (ii) Explain about the formation of ionic...
Text Solution
|
- (i) Define coordinate covalent bond. (ii) strate the formation of co...
Text Solution
|
- Explain the bond formation of hydrogen molecule.
Text Solution
|
- What are the important features of valence bond theory?
Text Solution
|
- Explain about sp hybridisation with suitable example.
Text Solution
|
- Explain the formation of methane using VB theory?
Text Solution
|
- Explain sp^(3) d hybridisation with a suitable example.
Text Solution
|
- Explain about sp^(3)d^(2) hybridisation with an example.
Text Solution
|
- Explain about the salient features of molecular orbital theory.
Text Solution
|
- Explain the MO diagram for NO molecule.
Text Solution
|
- Explain about metallic bonding.
Text Solution
|
- Explain about the salient features of molecular orbital theory.
Text Solution
|