रदरफोर्ड सोडी का रेडियो एक्टिव नियम- रदफोर्ड और सोडी ने रेडियो एक्टिव पदार्थों के लिए रेडियो क्षय का प्रयोगात्मक अधययन किया। अध्ययन के बाद निम्न नियम प्रतिपादित किया जिसे क्षय नियत कहते हैं। इस नियम के अनुसार-
1.रेडियोएक्टिव परमाणु के विघटन पर पदार्थ रासायनिक क्रिया इत्यादि का कोइ प्रभाव नहीं पड़ता। विघटन पूर्णतः स्वतः होता है। विघटन की घटना यादृच्छिक घटना होती है (अर्थात यह नही कहा जा सकता होगा) रेडियो एक्टिवता परमाणु के नाभिक का गुण होता है।
2.चरघातांकी क्षय का नियम- किसी भी रेडियोएक्टिव आसोटोप की निश्चित मात्रा में प्रति सेकण्ड विघटन होने वाले परमाणुओं की संख्या उस समय पर उपस्थित कुल सक्रिय परमाणुओं की संख्या पर निर्भर करती है। किसी समय विघटन की दर उस समय उपस्थित रेडियोएक्टिव नाभिकों की संख्या के अनुक्रमानुपाती होती है। इसे चारघातांकी क्षय का नियम कहते हैं।
क्षय समीकरण- माना किसी दिये गये नमूने में प्रारंभ में t=0 पर कुल सक्रिय परमाणुओं की संख्या `N_(0)`, समय t पर सक्रिय परमाणुओं की संख्या N तथा समय `(t+dt)` पर `(N-dN)` है अर्थात dt समय में dN परमाणु विघटित होते हैं तो
परमाणुओं के विघटन की दर `=-((dN)/(dt))`
प्रायिकता के नियम से `-((dN)/(dt))prop N`
या `(dN)/N=-lamdaN`…………..1
यहां `lamda` एक स्थिरांक है जिसे क्षयांक या विघटन स्थि)रांक कहते हैं।
समी 1 को व्यवस्थित करने पर
`(dN)/(N=-lamda dt`…….2
समी 2 का समाकलन करने पर
`int(dN)/N=-intlamda dt`
`:.log_(e)N=-lamdat+C`….3
जहां C एक नियतांक है C एक नियतांक है C का मान प्रारंभिक अवस्था से ज्ञात किया जाता है।
t=0 पर `N=N_(0)`
अतः समीकरण 3 से
`log_(e)N_(0)=0+C`
या `C=log_(e)N_(0)`……..4
समी 4 का मान समी 3 में रखने पर
`log_(e)N=-lamdat+log_(e)N_(0)`
या `log_(e)-log_(e)N_(0)=-lamdat`
`:.log_(e)(N/(N_(0)))=-lamdat` तथा `(N/(N_(0)))-e^(-lamdat)`…5
या `N=N_(0)e^(-lamdat)`…..6
समीकरण 6 को रेडियो एक्टिव क्षयता का नियम या विघटन का नियम या चारघातांकी क्षय का नियम कहते हैं। इस नियम के अनुसार रेडियोएक्टिव परमाणु का विघटन चरघातांकी रूप में होता है । चरघातांकी क्षय को चित्र में प्रदर्शित किया गया है।
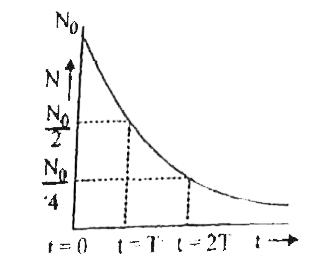
अर्द्ध आयु तथा माध्य आयु में संबंध
अर्ध आयु `T_(1//2)=0.693/(lamda)`
औसत आयु का माध्य आयु `T_(0)=1/(lamda`
`:.T_(1//2)=0.693xx1/(lamda)=0.693xxT_(0)`
या `T_(0)=0.693/(T_(1//2))`
अतः माध्य आयु `T_(0)=0.693/("अर्द्धआयु"(T_(1//2)))`
