Similar Questions
Explore conceptually related problems
Recommended Questions
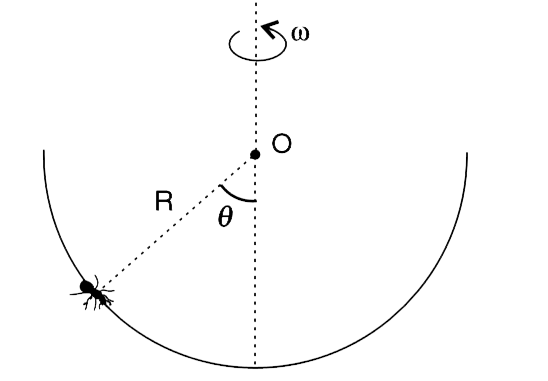
- A small insect is climbing slowly along the inner wall of a hemispheri...
Text Solution
|
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|
- The coefficient of friction between a hemispherical bowl and an insect...
Text Solution
|
- If the coefficient of friction between an insect and bowl is mu and th...
Text Solution
|
- A small insect is climbing slowly along the inner wall of a hemispheri...
Text Solution
|
- The coefficient of friction between an insect and a hemispherical bowl...
Text Solution
|
- The coefficient of friction between a hemispherical bowl and an insect...
Text Solution
|
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|