Similar Questions
Explore conceptually related problems
Recommended Questions
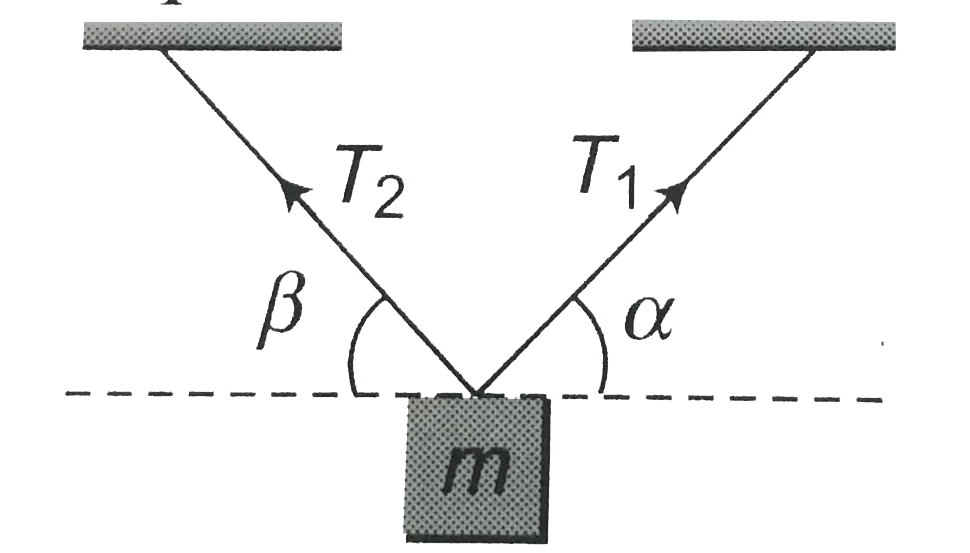
- The block is in equilibrium (i) T(1)=(mgcosbeta)/(sin(alpha+beta)...
Text Solution
|
- If the normals at points t1a n dt2 meet on the parabola, then t1t2=1 ...
Text Solution
|
- If alpha,beta,gamma are the roots of the equation x^(3)-2x^(2)-1=0 and...
Text Solution
|
- The block is in equilibrium (i) T(1)=(mgcosbeta)/(sin(alpha+beta))" "(...
Text Solution
|
- Calculate a, T(1), T(2), T(1)' & T(2)'.
Text Solution
|
- Let t(1)=(sin alpha)^(cos alpha), t(2)=(sin alpha)^(sin alpha), t(3)=(...
Text Solution
|
- If the tangents at t(1) and t(2) to a parabola y^2=4ax are perpendicul...
Text Solution
|
- Find the terms (s) indicated in each case: (i) t(n)=t(n-1)+3(ngt1),t...
Text Solution
|
- सारणिक |(1,cos(alpha-beta),cosalpha),(cos(alpha-beta),1,cosbeta),(cosa...
Text Solution
|