Similar Questions
Explore conceptually related problems
Recommended Questions
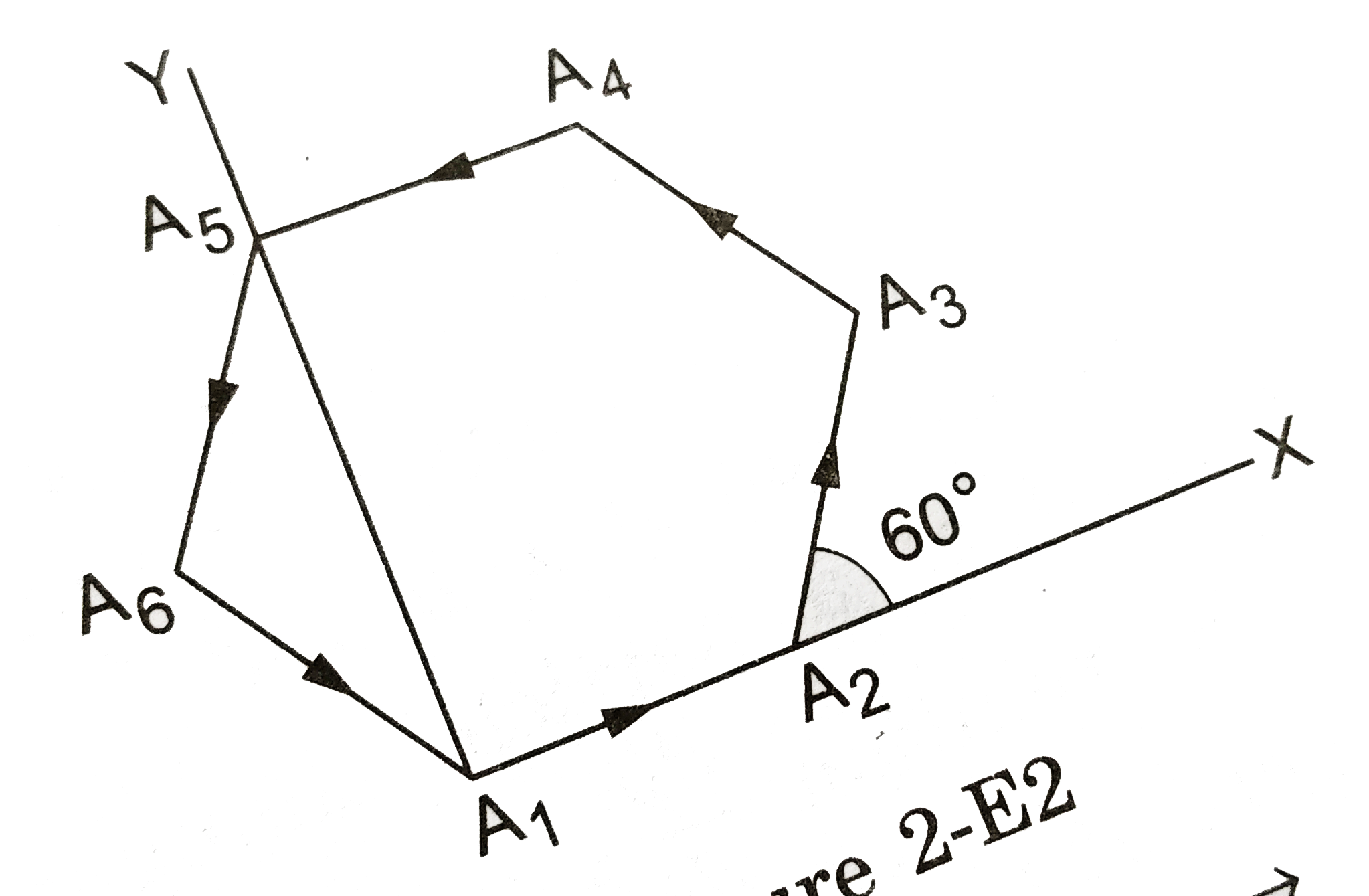
- Let A1 A2 A3 A4 A5 A6 A1 be a regular hexagon. Write the x-components ...
Text Solution
|
- If a1+a2+a3+......+an=1 AA a1 > 0, i=1,2,3,......,n, then find the ma...
Text Solution
|
- Let A1 A2 A3 A4 A5 A6 A1 be a regular hexagon. Write the x-components ...
Text Solution
|
- If ar=(cos2rpi+isin2rpi)^((1)/(9)), then the value of |{:(a1,a2,a3),(a...
Text Solution
|
- If (a2a3)/(a1a4) = (a2+a3)/(a1+a4)=3 ((a2 -a3)/(a1-a4)) then a1,a2, a3...
Text Solution
|
- క్రింది వానిని కనుగొనుము. a1 =-4, a6 = 6, అయిన a2, a3, a4, a5 లను కనుగ...
Text Solution
|
- క్రింది వానిని కనుగొనుము. a2 = 38, a6 = -22, అయిన a1, a3, a4, a5 లను క...
Text Solution
|
- यदि a1,a2……..a50गुणोत्तर श्रेणी में है तो (a1-a3+a5-….+a49)/(a2-a4+a6…...
Text Solution
|
- If a1+a2+a3+......+an=1 AA ai > 0, i=1,2,3,......,n, then find the ma...
Text Solution
|
 .
.