Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-VECTOR ALGEBRA -CHAPTER TEST 10
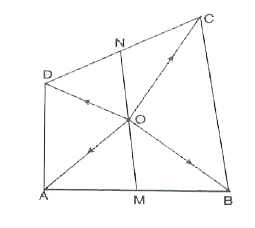
- In the figure, M is the mid - point of [AB] and N is the mid - point o...
Text Solution
|
- What is the area of the rectangle having vertices A, B, C and D with p...
Text Solution
|
- Write the value of hat(i).(hat(j)xxhat(k))+hat(j).(hat(i)xxhat(k))+ha...
Text Solution
|
- Find the value of x for which x( hat i+ hat j+ hat k)is a unit vector...
Text Solution
|
- Find the angle between the vectors hat(i)-hat(j) and hat(j)-hat(k).
Text Solution
|
- Find |vec(a)xx vec(b)|, if vec(a)=2hat(i)+hat(j)+3hat(k) and vec(b)=3...
Text Solution
|
- Show that the vectors 2 hat i-3 hat j+4 hat k\ a n d-4 hat i+6 hat j-8...
Text Solution
|
- Show that the vectors 2 hat i- hat j+ hat k , hat i-3 hat j-5 hat kan...
Text Solution
|
- If |a|=a and | vec b|=b , prove that ( vec a/( vec a^2)- vec b/(b^2))^...
Text Solution
|
- If vec(r )=x hat(i)+y hat(j)+x hat(k), find : (vec(r )xx hat(i)).(vec...
Text Solution
|
- Find the value of 'lambda' such that vectors : 3hat(i)+lambda hat(j)+5...
Text Solution
|
- Let vec a ,\ vec b ,\ vec c be three vectors of magnitudes 3, 4 and...
Text Solution
|
- Prove by vector method that sin(A-B)=sinAcosB-cosAsinB and sin(A+B)=si...
Text Solution
|