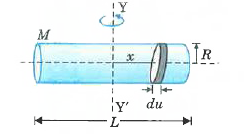
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
MODERN PUBLICATION|Exercise COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )|35 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
MODERN PUBLICATION|Exercise COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )|10 VideosSYSTEMS OF PARTICLES AND ROTATIONAL MOTION
MODERN PUBLICATION|Exercise COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MULTIPLE CHOICE QUESTIONS) (MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER) )|67 VideosPHYSICAL WORLD
MODERN PUBLICATION|Exercise Revision exercises (Long answer questions)|6 VideosTHERMAL PROPERTIES OF MATTER
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|15 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
- The coordinates of a particle of mass 'm' as function of time are give...
Text Solution
|
- A thin disc of mass M and radius R has mass per unit area sigma( r) =k...
Text Solution
|
- A cubical block of side a is moving with velocity V on a horizontal sm...
Text Solution
|
- Cement, sand and seree are dropped in rotating cylidrical drum to make...
Text Solution
|
- In the figure shown ABC is a uniform wire. If centre of mass of wire l...
Text Solution
|
- A uniform disc of radius R and mass M is free to rotate only about its...
Text Solution
|
- Moment of inertia of an equilateral triangular lamina ABC, about the a...
Text Solution
|
- The machine as shown has 2 rods of length 1 m connected by a pivot at ...
Text Solution
|
- A disc has mass 9 m. A hole of radius R/3 is cut from it as shown in t...
Text Solution
|
- The moment of inertia of a uniform cylinder of length l and radius R a...
Text Solution
|
- Two coaxial discs, having moments of inertia l(1) and (I(1))/(2) are r...
Text Solution
|
- A disc has mass 9 m. A hole of radius R/3 is cut from it as shown in t...
Text Solution
|
- A particle moves in circular path with decreasing speed. Which of the ...
Text Solution
|
- A solid sphere of mass M and radius R having tmoment of inertia I abou...
Text Solution
|
- A small object of uniform density rolls up a curved surface with an in...
Text Solution
|
- Two discs A and B are mounted coaxiallay on a vertical axle. The discs...
Text Solution
|
- In the above question disc B is brought in contact with disc A, they a...
Text Solution
|
- Two discs A and B are mounted coaxially on a vertical axle. The discs ...
Text Solution
|
- A ring of mass M and radius R is rotating with angular speed omega abo...
Text Solution
|
- A uniform wooden stick of mass 1.6 kg and length l rests in an incline...
Text Solution
|