Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROSTATIC POTENTIAL AND CAPACITANCE
MODERN PUBLICATION|Exercise NCERT FILE Solved (Textbook Exercise)|11 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
MODERN PUBLICATION|Exercise NCERT FILE Solved (Additional Exercises)|23 VideosELECTROSTATIC POTENTIAL AND CAPACITANCE
MODERN PUBLICATION|Exercise Conceptual Questions|37 VideosELECTROMAGNETIC WAVES
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|14 VideosMAGNETISM AND MATTER
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|16 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-ELECTROSTATIC POTENTIAL AND CAPACITANCE -Tough & Tricky PROBLEMS
- There is one parallel plate capacitor of plate area A and separation b...
Text Solution
|
- In the figure given below there is one parallel plate capacitor with t...
Text Solution
|
- Consider the network of capacitors as shown in the figure. Find equiva...
Text Solution
|
- Consider the following circuit with a switch S(w). Potential differenc...
Text Solution
|
- Consider a thick walled metallic spherical shell with inner radius a a...
Text Solution
|
- There are three concentric metallic spherical shells of radius a, b an...
Text Solution
|
- There are three concentric metallic spherical shells of radius R, 2R a...
Text Solution
|
- Twelve identical capacitors of capacitance C are connected across each...
Text Solution
|
- Twelve capacitors, each having a capacitance C, are connected to form ...
Text Solution
|
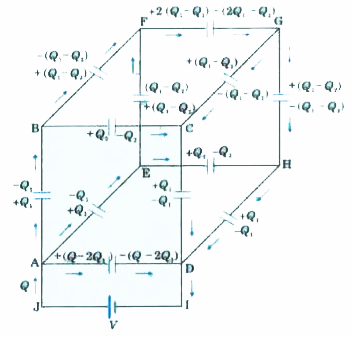
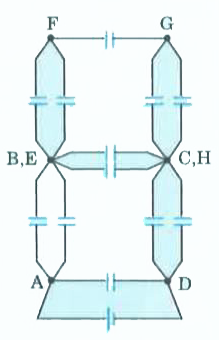
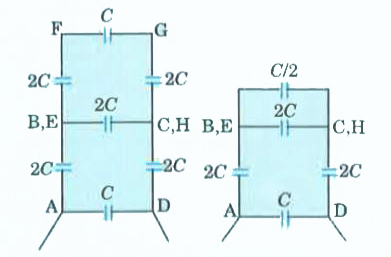
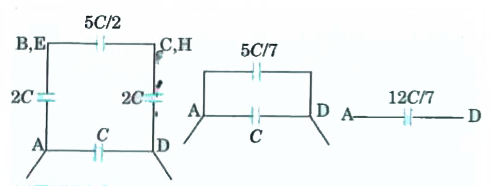
- Twelve identical capacitors of capacitance C are connected across each...
Text Solution
|