Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROMAGNETIC INDUCTION
MODERN PUBLICATION|Exercise REVISION EXERCISE (Very Short Answer Questions Carrying I mark)|44 VideosELECTROMAGNETIC INDUCTION
MODERN PUBLICATION|Exercise REVISION EXERCISE (Additional Questions (Carrying I mark))|11 VideosELECTROMAGNETIC INDUCTION
MODERN PUBLICATION|Exercise NCERT FILE (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS) (Short answer type questions)|5 VideosELECTRIC CHARGES AND FIELDS
MODERN PUBLICATION|Exercise Chapter Practice Test|15 VideosELECTROMAGNETIC WAVES
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|14 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-ELECTROMAGNETIC INDUCTION-HIGHER ORDER THINKING SKILLS AND ADVANCED LEVEL
- Two vertical metal rails are connected at the top through a capacitor ...
Text Solution
|
- Inductors of self-inductances L(1) and L(2) having resistances R(1) an...
Text Solution
|
- There are two circular coils P and Q placed coaxially at a distance x ...
Text Solution
|
- A ring of insulated material and radius R is kept on a frictionless ho...
Text Solution
|
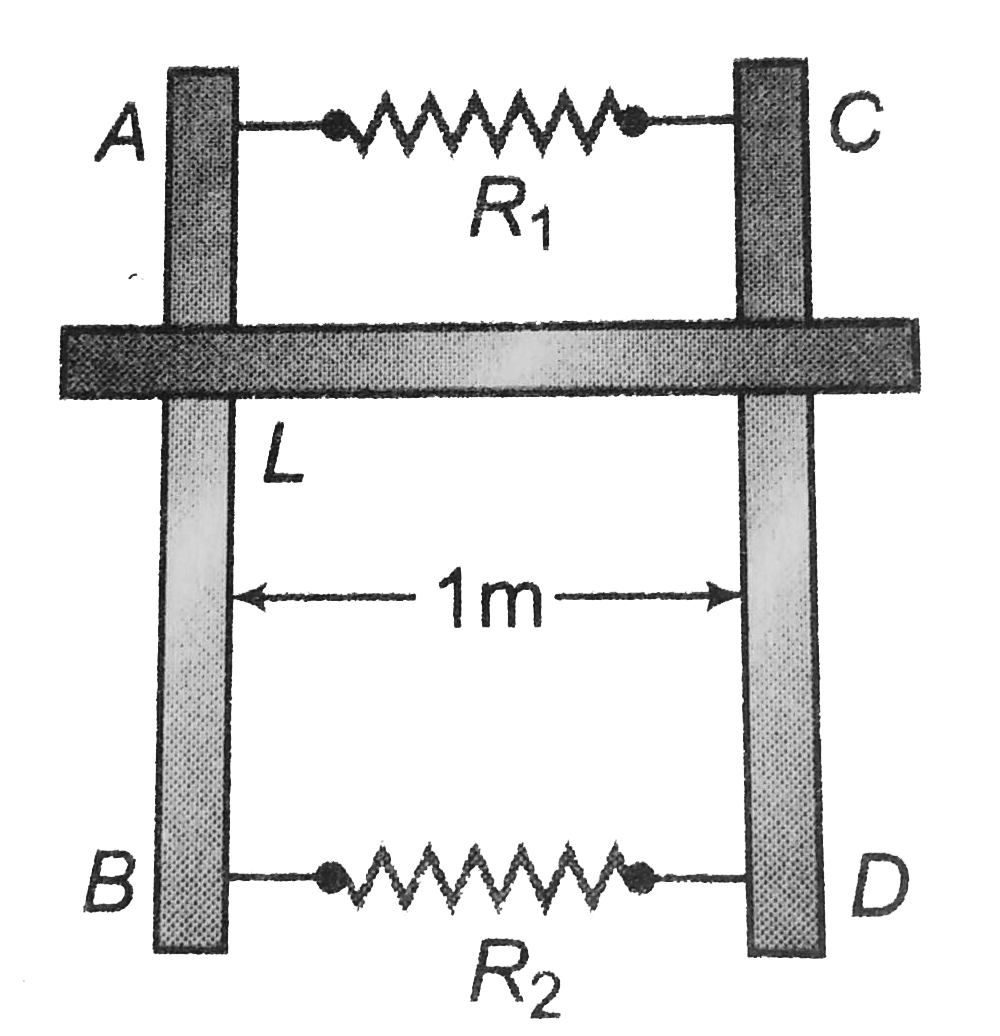
- Two parallel vertical metallic rails AB and CD are separated by 1m. Th...
Text Solution
|
- A square loop of edge a, and a long straight conductor carrying curren...
Text Solution
|
- There is one long coaxial cable which consists of two concentric cylin...
Text Solution
|
- There is small circular coil which is suspended through a wire of leng...
Text Solution
|