Text Solution
Verified by Experts
Topper's Solved these Questions
WAVE OPTICAL
MODERN PUBLICATION|Exercise NCERT FILE SOLVED (TEXT BOOK EXERCISES)|10 VideosWAVE OPTICAL
MODERN PUBLICATION|Exercise NCERT FILE SOLVED (Additional Exercises)|11 VideosWAVE OPTICAL
MODERN PUBLICATION|Exercise Conceptual Questions|23 VideosSEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|12 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-WAVE OPTICAL-Tough & Tricky (PROBLEMS)
- Two thin glass plates are placed parallel to each other such that dist...
Text Solution
|
- Two slits are made on an opaque surface at a separation of 1 mm from e...
Text Solution
|
- In Young's experiment the upper slit is covered by a thin glass plate ...
Text Solution
|
- In a modified Young's double-slit experiment, a monochromatic uniform ...
Text Solution
|
- White light is incident on water film of thickness 1 mu m. Refractive ...
Text Solution
|
- Soap film of thickness 1 mu m appears bright when seen through reflect...
Text Solution
|
- White light is incident on a very thin glass plate of thickness 1 mu m...
Text Solution
|
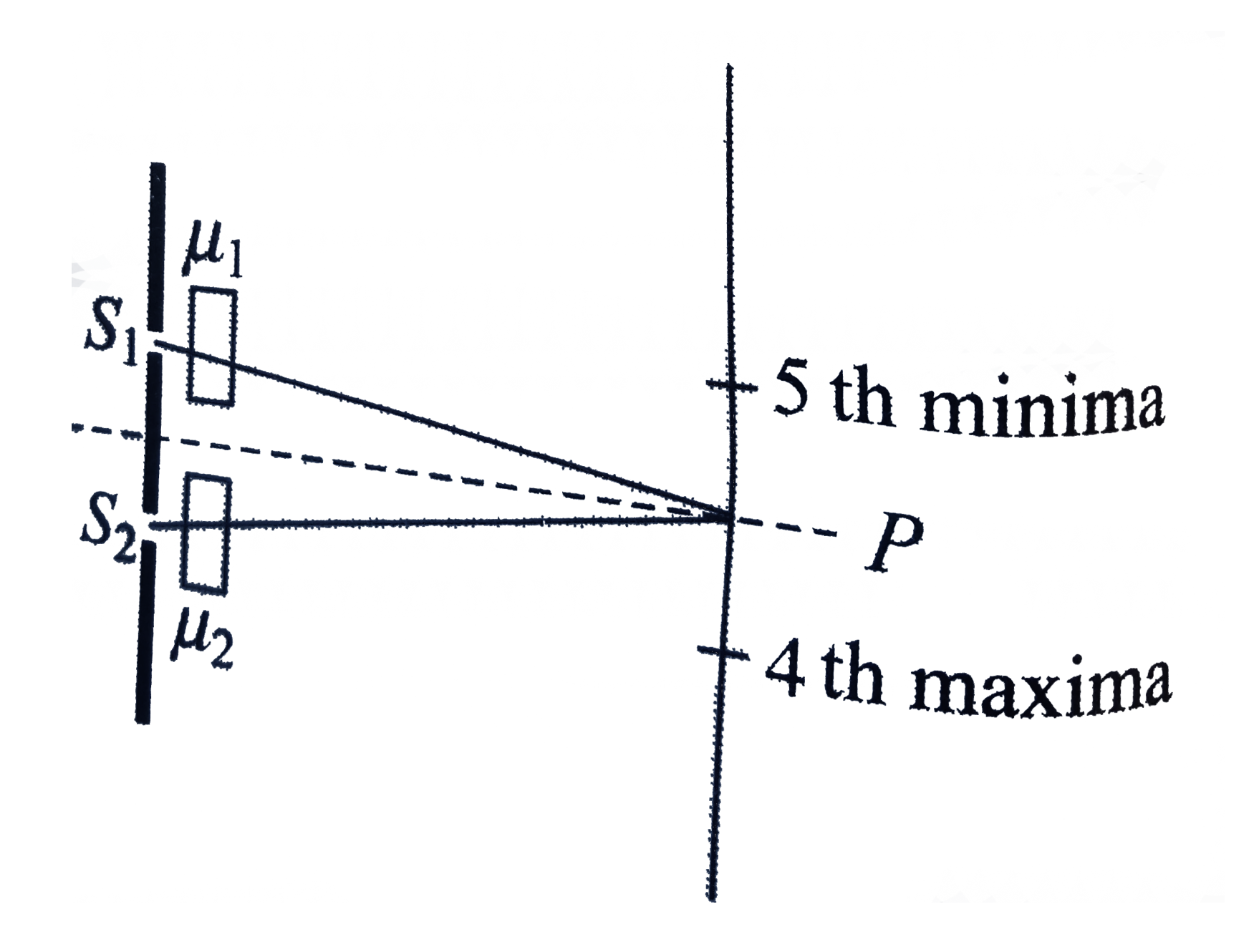 .
.