Text Solution
Verified by Experts
Topper's Solved these Questions
WAVE OPTICAL
MODERN PUBLICATION|Exercise Revision Exercises (Very Short Answer Questions)|51 VideosWAVE OPTICAL
MODERN PUBLICATION|Exercise Revision Exercises (Additional Questions)|12 VideosWAVE OPTICAL
MODERN PUBLICATION|Exercise NCERT (Exemplar Problems Subjective Questions) (Short Answer Type Questions)|3 VideosSEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|12 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-WAVE OPTICAL-Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)
- Let I1 and I2 be intensities of two sources such that (I1)/(I2) = k. F...
Text Solution
|
- Monichromatic lightof wavelenght 600 nm is used ina Young's double sli...
Text Solution
|
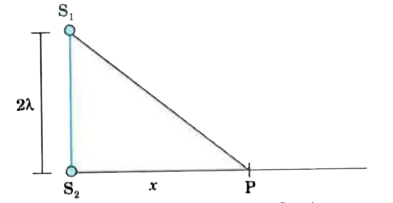
- Two coherent point sources S(1) and S(2) vibrating in phase emit light...
Text Solution
|
- Calculate the smallest angular separation between two stars which are ...
Text Solution
|
- Oil film of thickness 1 mu m is deposited on a glass plate. Refractive...
Text Solution
|
- Separation between the slits of YDSE set-up is 0.1 cm. Films of same t...
Text Solution
|
- In Young's double-slit experiment, two coherent source are used. Inten...
Text Solution
|
- In a Young's double slit experiment using monochromatic light, the fri...
Text Solution
|
 .
.