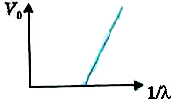A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
DUAL NATURE OF RADIATION AND MATTER
MODERN PUBLICATION|Exercise COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( D - Multiple Choice Questions) )|5 VideosDUAL NATURE OF RADIATION AND MATTER
MODERN PUBLICATION|Exercise COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS))|11 VideosDUAL NATURE OF RADIATION AND MATTER
MODERN PUBLICATION|Exercise COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( B - Multiple Choice Questions) (JEE (Advanced) for IIT Entrance))|15 VideosCURRENT ELECTRICITY
MODERN PUBLICATION|Exercise Chapter Practice Test|15 VideosELECTRIC CHARGES AND FIELDS
MODERN PUBLICATION|Exercise Chapter Practice Test|15 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-DUAL NATURE OF RADIATION AND MATTER -COMPETITION FILE (OBJECTIVE TYPE QUESTIONS ( C - Multiple Choice Questions) )
- If an electron and a photon propagate in the form of waves having the...
Text Solution
|
- A parallel beam of negatively charged particles is illuminated normall...
Text Solution
|
- Photon having energy E has the same de Broglie wavelength as that of p...
Text Solution
|
- Which of the following is correct ?
Text Solution
|
- A metallic surface is irradiated with light energy E , of wave length ...
Text Solution
|
- In photoelectric effect,
Text Solution
|
- The graph between the stopping potential (V(0)) and ((1)/(lambda)) is...
Text Solution
|
- For photoelectric effect with incident photon wavelength lamda, the st...
Text Solution
|