Home
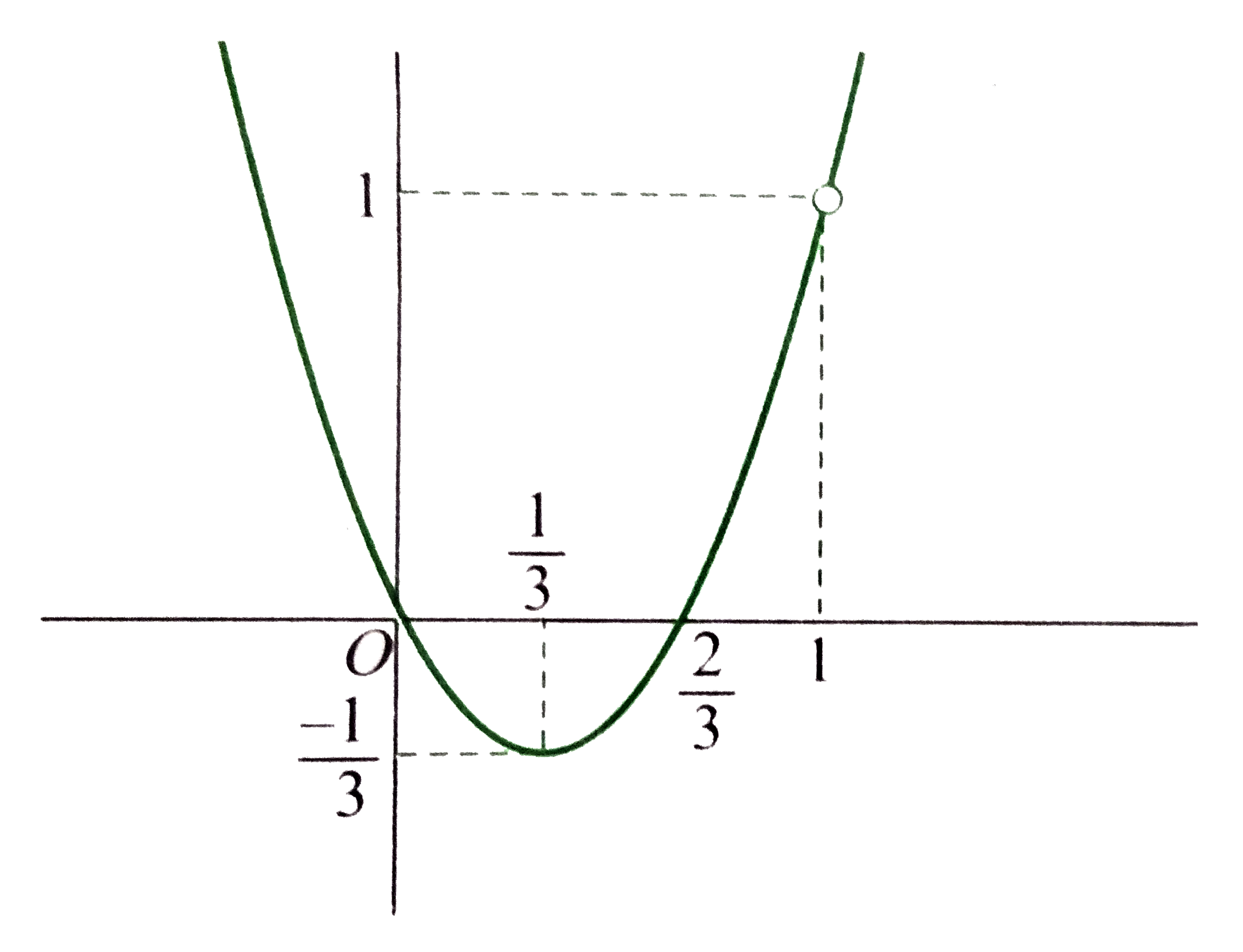
Class 12
MATHS
If a in R and the equation -3(x-[x])^2+2...

If `a in R` and the equation `-3(x-[x])^2+2(x-[x])+a^2=0` (where [x] denotes the greatest integer `le x`) has no integral solution, then all possible values of a lie in the interval: (1) (-2,-1) (2) `(oo,-2) uu (2,oo)` (3) `(-1,0) uu (0,1)` (4) (1,2)

A

`(-1,0) cup (0,1)`

B

`(1,2)`

C

`(-2,-1)`

D

`(-oo,-2)cup (2,oo)`

Text Solution

Verified by Experts

The correct Answer is:
A
`a^(2)=3t^(2)-2t, " where " t={x} in [0,1)`
` :. a^(2) =3t(t-2//3)`
Graph of `f(t)=3t(t-2//3)` is as shown in the following figure.

Clearly, from graph
`0 lt a^(2) lt 1`
`or a in (-1,0) cup (0,1) `
Promotional Banner

Topper's Solved these Questions

  • RELATIONS AND FUNCTIONS

    CENGAGE|Exercise Solved Examples And Exercises|498 Videos

  • RELATIONS AND FUNCTIONS

    CENGAGE|Exercise Exercise (Numerical)|31 Videos

  • Quadratic Equations, Inequalities, Modulus and Logarithms

    CENGAGE|Exercise Question Bank|31 Videos

  • SCALER TRIPLE PRODUCTS

    CENGAGE|Exercise DPP 2.3|11 Videos

Similar Questions

Explore conceptually related problems

If a in R and the equation -3(x-[x])^2+""2""(x-[x])""+a^2=""0 (where [x] denotes the greatest integer x) has no integral solution, then all possible values of a lie in the interval (1) (-1,""0)uu(0,""1) (2) (1, 2) (3) (-2,-1) (4) (-oo,-2)uu(2,oo)

If a in R and the equation (a-2) (x-[x])^(2) + 2(x-[x]) + a^(2) = 0 (where [x] denotes the greatest integer function) has no integral solution and has exactly one solution in (2, 3), then a lies in the interval

If [x] denotes the greatest integer le x , then number of solutions of the equation x^(2) - 2 - 2 [x] =0 is

The value of the integral, int_1^3 [x^2-2x–2]dx , where [x] denotes the greatest integer less than or equal to x, is :

If (x)={x[x],0<=x<=2 and (x-1)[x],2<=x<=3,where [x] denotes the greatest integer function, then

Evaluate int_(0)^(oo)[(3)/(x^(2)+1)]dx where [.] denotes the greatest integer function.

Find the values of x graphically satisfying [x]-1+x^(2)le0 where [.] denotes the greatest integer function.

If [x] denotes the greatest integer less than or equal to x, then evaluate lim_(n rarr oo)(1)/(n^(3)){[1^(2)x]+[2^(2)x]+[3^(2)x]+...}[n^(2)x]}

The domain of f(x)=log_((1)/(2))log_(4)log_(4)[x-lambda]^(2) (where [1 denotes the greatest integer function is (-oo,2]uu[6,oo) then the value of lambda is