A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CENGAGE-AREA-Exercise (Comprehension)
- Let A(r) be the area of the region bounded between the curves y^(2)=(e...
Text Solution
|
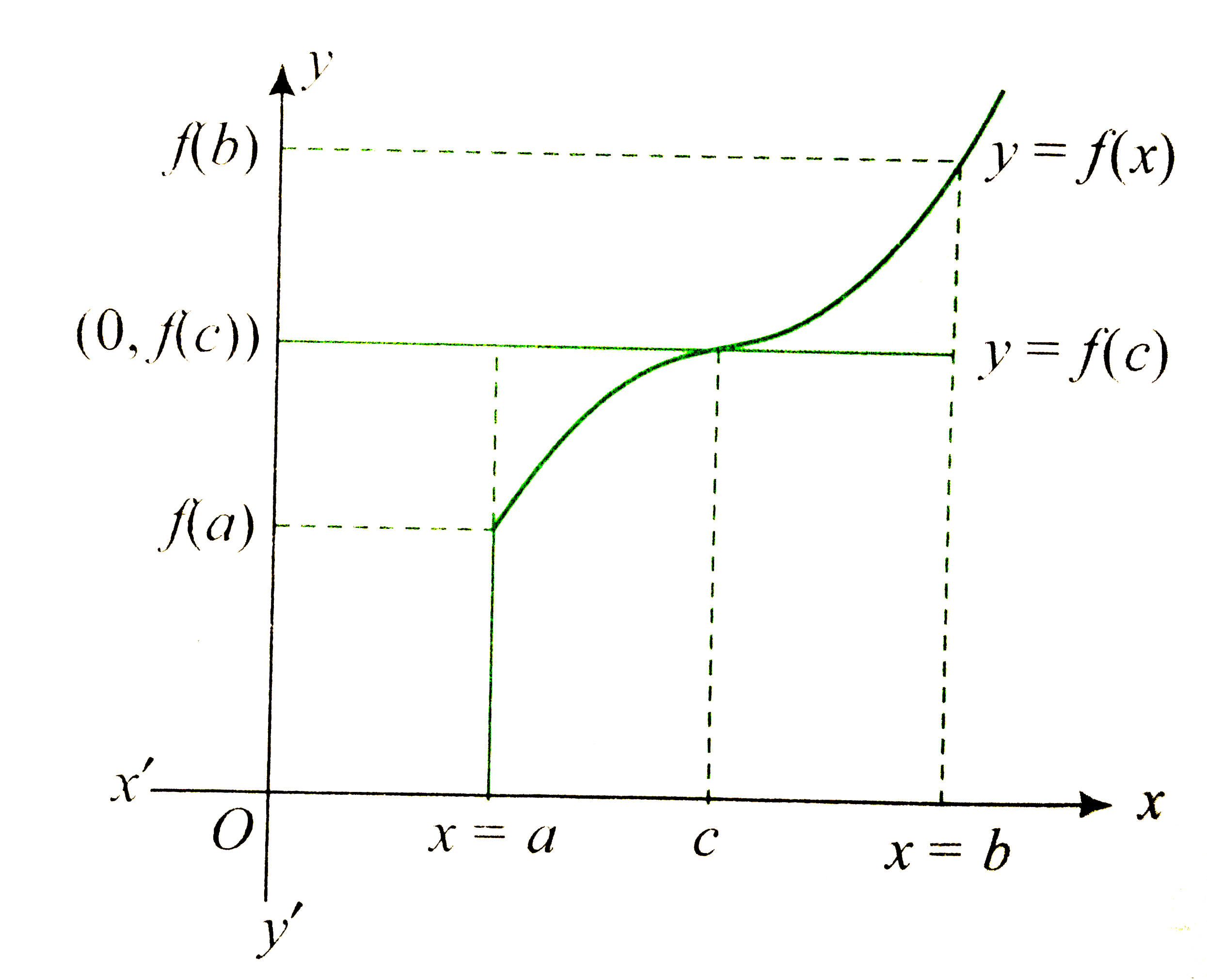
- If y=f(x) is a monotonic function in (a,b), then the area bounded by t...
Text Solution
|
- If y=f(x) is a monotonic function in (a,b), then the area bounded by t...
Text Solution
|
- If y=f(x) is a monotonic function in (a,b), then the area bounded by t...
Text Solution
|
- Consider the area S(0),S(1),S(2)…. bounded by the x-axis and half-wave...
Text Solution
|
- Consider the sequence of natural numbers s0,s1,s2,... such that s0 =3,...
Text Solution
|
- Consider the area S(0),S(1),S(2)…. bounded by the x-axis and half-wave...
Text Solution
|
- "Two curves "C(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C(2)equiv[f(y)...
Text Solution
|
- "Two curves "C(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C(2)equiv[f(y)...
Text Solution
|
- "Two curves "C(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C(2)equiv[f(y)...
Text Solution
|
- Consider the two curves C(1):y=1+cos x and C(2): y=1 + cos (x-alpha)" ...
Text Solution
|
- Consider two curves C1:y =1/x and C2.y=lnx on the xy plane. Let D1, de...
Text Solution
|
- Consider the function defined implicity by the equation y^(2)-2ye^(sin...
Text Solution
|
- Consider the function defined implicity by the equation y^(2)-2ye^(sin...
Text Solution
|
- Consider two functions f (x) ={[x] , -2 leq x leq -1 and |x|+1 , -1 ...
Text Solution
|
- Computing area with parametrically represented boundaries : If the bou...
Text Solution
|
- Computing area with parametrically represented boundaries : If the bou...
Text Solution
|
- Computing area with parametrically represented boundaries : If the bou...
Text Solution
|
- Let f(x) be a continuous function fiven by f(x)={(2x",", |x|le1),(x^(2...
Text Solution
|
- Let f(x) be continuous function given by f(x)={2x ,|x|lt=1x^2+a x+b ,|...
Text Solution
|